Problema 125.- Sea P un punto del arco menor AB de la circunferencia circunscrita del triángulo equilátero ABC. Se tiene que, CP=AP+BP.
(Yiu P. (1998):"Euclidean Geometry" 1998. p.150 )
Solución de Saturnino Campo Ruiz.-
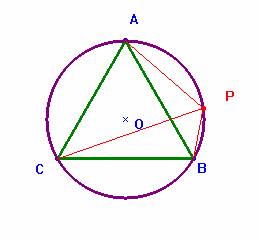El teorema de Ptolomeo aplicado al cuadrilátero inscriptible
ABCP, nos da que el producto de sus diagonales es igual a la suma
de los productos de los lados opuestos, esto es, AB·PC
= AC·PB + BC·PA. Dividiendo
por el valor común del lado del triángulo se obtiene la relación buscada:
PC = PB + PA.