Problema 126
Sea P un punto de la circunferencia inscrita al triángulo equilátero ABC de lado a.
Se tiene que: AP² + BP² + CP² = 5(a/2)²

Sugerencia del editor:
Si P es de la circunferencia circunscrita, se tiene que AP² + BP² + CP² = 2a²

Yiu P. (1998):"Euclidean Geometry" 1998. p.150

Solución de F. Damián Aranda Ballesteros.

Trazamos los segmentos PA, PB y PC y construimos el triángulo medial A'B'C', que estará inscrito en la circunferencia inscrita del triángulo ABC inicial.

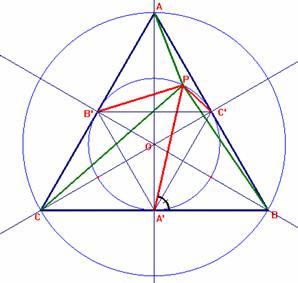
Aplicando el teorema de los cosenos para el triángulo APB', por un lado y PB'C por otro y sumando obtenemos:

PA² + PC² = 2×PB'² + 2× (a/2)²

De igual manera, para los triángulos APC', por un lado y PC'B, por otro, obtenemos:

PA² + PB² = 2×PC'² + 2× (a/2)²

Finalmente, para el par de triángulos CPA', por un lado y BPA', por otro, obtenemos:

PC² + PB² = 2×PA'² + 2× (a/2)²

En resumidas cuentas, tenemos las relaciones cíclicas siguientes:

PA² + PC² = 2×PB'² + 2× (a/2)²

PA² + PB² = 2×PC'² + 2× (a/2)²

PC² + PB² = 2×PA'² + 2× (a/2)²

Si las sumamos todas ellas, resultará:

2×( PA² + PB² + PC² ) = 2×(PA'² + PB'² + PC'² ) + 6× (a/2)²

PA² + PB² + PC² = PA'² + PB'² + PC'² + 3× (a/2)²

Ahora bien, PA'² + PB'² + PC'² = 2×(a/2)²

Así tenemos finalmente: PA² + PB² + PC² = 5×(a/2)²

Nota. Justificamos la sugerencia del editor:
Si P es de la circunferencia circunscrita, se tiene que AP² + BP² + CP² = 2a²

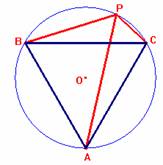Tenemos probado por el problema 125, que AP = BP + CP. Aplicando el teorema de los cosenos al triángulo PBC, tenemos que: a² = BP + CP²-2×BP×CP×cos120º, es decir

a² = BP² + CP² + BP×CP

De este modo:
AP² + BP² + CP² = (BP + CP)² + BP² + CP² ;
AP+ BP² + CP² = 2×(BP² +CP² +BP×CP) = 2×a²