------------------------------------------------------

Propuesta del profesor Ricard Peiró, del IES 1 de Cheste

Problema 126

Problema 126

Sea P un punto de la circunferencia inscrita al triángulo equilátero ABC de lado a. Se tiene que AP²+BP²+CP²=5(a/2)²

Sugerencia del editor: Si P es de la circunferencia circunscrita, se tiene que AP²+BP²+CP²=2a²

 circunferencia inscrita al triángulo equilátero ABC de lado a.

Se tiene que AP²+BP²+CP²=5(a/2)²

Yiu P. (1998):"Euclidean Geometry" 1998. p.150

Solución de Maite Peña Alcaraz:

Si centramos el triángulo equilátero en los ejes cartesianos y dando al radio de la circunferencia circunscrita valor 1, el de la inscrita tendría valor 1/2, obtenemos:

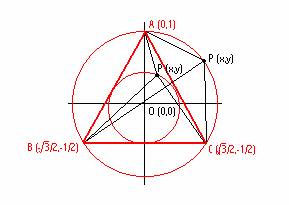
En general, PA²= x²+(y-1)², PB²= (x+(3^(½))/2)²+(y+½)² y PC²= (x-(3^(½))/2)²+(y+½)² ; y sumándolos y operando se obtiene que PA²+PB²+PC²=3x²+3y²+3. Ahora, en cada apartado:

a)     En este caso, la ecuación de la circunferencia inscrita es x²+y²=1/4, por tanto, PA²+PB²+PC²=3x²+3y²+3=3x²+3(1/4-x²)+3=15/4 independientemente del valor de x, y como el lado de este triángulo vale (3/2)/sen60º=3^(½) se cumple la igualdad propuesta.

b)     En este caso, la ecuación de la circunferencia circunscrita es x²+y²=1 luego PA²+PB²+PC²=3x²+3y²+3=3x²+3(1-x²)+3=6 y puesto que el lado es igual a raíz cuadrada de tres se cumple la igualdad.

------------------------------------------------------------