Problema 127
Dado un triángulo arbitrario OAB, se forma un triángulo en los lados que generan a OAB de vectores tOA, sAB y rOB con origen en O, A y O respectivamente.
La razón entre las áreas del triángulo inicial y el nuevo es [ | s(t-r)- t×r + r | ] ^-1.

Rosillo, N. (2003): Comunicación personal.

Solución de F. Damián Aranda Ballesteros.

Nota: Consideramos sólo el caso particular en el que el triángulo construido tiene sus vértices sobre los lados del triángulo ABC y no sobre las rectas que lo determinan.

En concreto, consideramos la situación reflejada en la siguiente figura:

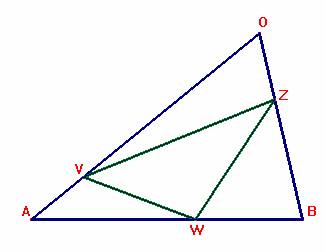En ella, observamos que:

0<t<1; 0<s<1; 0<r<1

La relación entre las áreas S₁, S₂, S₃, S₄ y S de los triángulos OVZ, AVW, BWZ, VWZ y ABC es la siguiente: S₁ + S₂ + S₃ + S₄ = S.

Por tanto,
S₁ + S₂ + S₃ + S₄ = S ;

Es decir:

t×r×S + s×(1-t)×S + (1-s)×(1-r)×S + S₄ = S;

En definitiva,

S₄ = S×(1- t×r - s×(1-t) - (1-s)×(1-r));