Problema 131.-
Dividir el perímetro de un triángulo en dos triángulos con
el mismo perímetro por una ceviana. Tal ceviana se denomina escisor. Los tres
escisores de un triángulo se cortan en un punto llamado de Nagel.
Honsberger, R. (1995): Episodes in 19 & 20 C Euclidean Geomtry. MAA (p.
5)
Solución de F. Damián Aranda Ballesteros
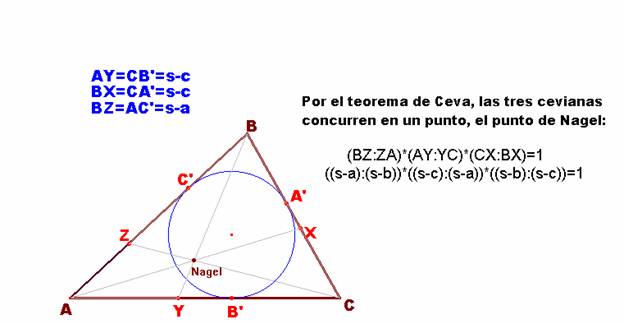
Supongamos situado el punto X en el lado BC de modo que la ceviana AX divida al triángulo inicial ABC en dos triángulos de igual perímetro.
Entonces se dará la siguiente relación:
BX + AB = XC + AC, o lo que es lo mismo:
BX + c = (a - BX) + b; BX = (a+b-c)/2 = s-c
En definitiva, una vez construida la circunferencia inscrita al triángulo ABC, se toma el segmento s-c = CB’ sobre el lado BC a partir del vértice B. Así construimos el escisor desde A. De similar modo se construyen los escisores desde B y C.
Que los tres escisores se cortan en un punto, punto de Nagel, es consecuencia directa del teorema de Ceva.