Problema 131.- Dividir el perímetro de un triángulo en
dos triángulos con el mismo perímetro por una ceviana. Tal ceviana se denomina
escisor. Los tres escisores de un triángulo se cortan en un punto llamado
de Nagel.
Honsberger, R. (1995): Episodes in 19 &
Solución del profesor Saturnino Campo Ruiz. IES Fray Luis de León. Salamanca.-
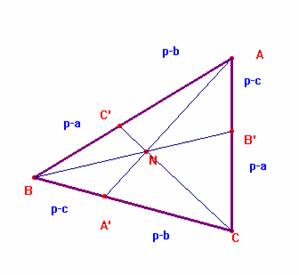
Si elegimos el punto A’ sobre el lado BC, se ha de verificar que los perímetros de los triángulos en que se divide el original por la ceviana AA’ sean iguales. Si no se toma la longitud de esta ceviana, los otros dos lados deben sumar el semiperímetro p del triángulo, por tanto, el segmento B’A’ debe medir p-c mientras que A’C medirá p-b. El mismo razonamiento con cada lado del triángulo no lleva a la distribución de los puntos A’, B’ y C’ como se muestran en la figura.
Para la concurrencia de los tres escisores
en el punto de Nagel, N bastará con la aplicación del teorema de
Ceva: 
= (p-c)/(p-b)·(p-a)/(p-c)·(p-b)/(p-a)
= 1.
Según explicamos en el problema nº 110, los puntos de tangencia de las circunferencias inscrita y exinscrita son simétricos respecto al pie de la mediana, y por tanto, la posición de los tres escisores A’, B’ y C’ es justamente la de los puntos de tangencia de las circunferencias exinscritas.