problema 131. Solución de William Rodríguez Chamache profesor de Geometríade la "Academia integral class" Trujillo- Perú

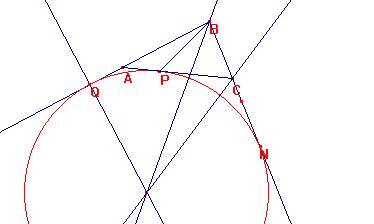
Dividir el perímetro de un triángulo en dos triángulos con el mismo
perímetro por una ceviana.

-por propiedad se sabe que PC=CN=m y sea BC=n

dela misma manera: AP=AQ=a y sea AB=b

finalmente se sabe que BQ=BN por lo tanto: a+b= m+n y los perimetros

de los
triángulos ABP y BPC son iguales.

problema 131-2

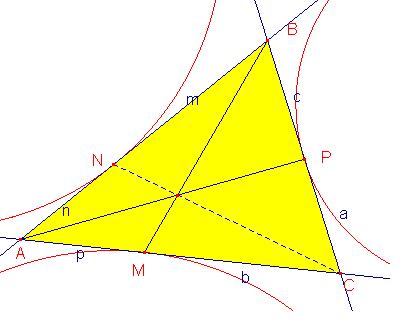
se sabe que: a+c+b=m+n+p
de igual manera : m+n+c=p+b+a
sumando estas dos ecuaciones obtenemos: c=p, de igual manera a=n y b=m
finalmente por el teorema de ceva se cumple que: n.c.b=m.a.p
por lo tanto los tres escisores se cortan en un punto K llamado punto de
Nagel.