Problema 133.-
Dividir un triángulo en dos figuras,
un cuadrilátero y un triángulo de la misma área por
un punto que no sea vértice ni punto medio de un lado.
Barroso, R. (2004) Comunicación personal
Solución de F. Damián Aranda Ballesteros
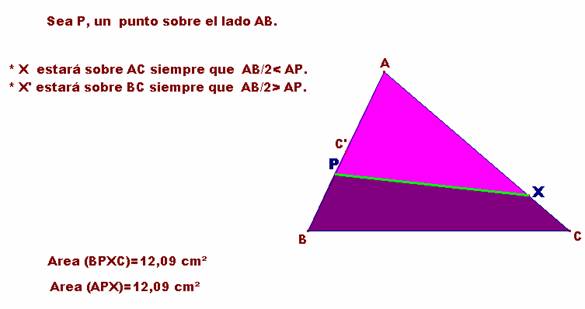
Sean dados el triángulo ABC y un punto cualquiera P sobre AB.
Consideramos dos casos según que P esté situado entre B y C’ o entre C’y A,
siendo C’ el punto medio del lado AB.
* P está situado entre B y C’.
Entonces se ha de verificar que 1/4∙c∙b∙senA=
1/2∙AP∙AX∙senA;
Así se tiene que verificar que: AX= ![]() .
.
En definitiva, AX es la cuarta proporcional de los segmentos 2∙AP; c
y b, cuya construcción es trivial.
Observamos que para determinar el punto X se ha de verificar
que AX= ![]() <AC=
b , es decir, c/2< AP, lo cual ocurre sii P está situado entre B y C’.
<AC=
b , es decir, c/2< AP, lo cual ocurre sii P está situado entre B y C’.
* P está situado entre A y C’.
Entonces se ha de verificar que 1/4∙c∙a∙senB=
1/2∙BP∙BX’∙senB; Así se tiene que verificar que: BX’=
![]() .
.
En definitiva, BX’ es la cuarta proporcional de los segmentos 2∙BP;
c y a, cuya construcción es trivial.
Observamos que para determinar el punto X’ se ha de verificar
que BX’= ![]() <BC=a
, es decir, c/2< BP, lo cual ocurre sii P está situado entre A y C’.
<BC=a
, es decir, c/2< BP, lo cual ocurre sii P está situado entre A y C’.