Problema 133:
Dividir un triángulo en dos figuras, un cuadrilátero y un triángulo de la misma área por un punto que no sea vértice ni punto medio de un lado.
Solución del profesor Nicolás Rosillo. IES Máximo Laguna. Sta Cruz de Mudela (17 de enero de 2004)
Se distinguen dos configuraciones a las cuales puede reducirse cualquier otra:
|
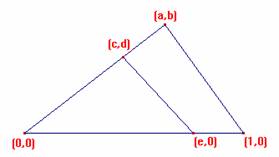
CASO 1. e<0,5 |
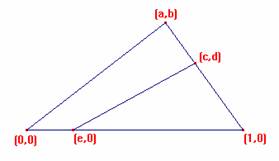
CASO 2. e>0,5 |
CASO 1
Para que se cumplan las condiciones pedidas se deben satisfacer las siguientes ecuaciones:
![]() (el
punto (c,d) perteneciente al lado
del triángulo)
(el
punto (c,d) perteneciente al lado
del triángulo)
![]() (el
área del triángulo es igual al área del cuadrilátero, obtenida esta última
como suma de dos triángulos).
(el
área del triángulo es igual al área del cuadrilátero, obtenida esta última
como suma de dos triángulos). ![]() da
soluciones fuera de los lados del triángulo.
da
soluciones fuera de los lados del triángulo.
Si se resuelve el sistema formado por estas dos ecuaciones en c y d, se obtiene
![]()
CASO 2
![]() (el
punto (c,d) pertenece al lado del
triángulo)
(el
punto (c,d) pertenece al lado del
triángulo)
![]() (el
área del triángulo es igual al área del cuadrilátero, obtenida esta última
como suma de dos triángulos).
(el
área del triángulo es igual al área del cuadrilátero, obtenida esta última
como suma de dos triángulos). ![]() da
soluciones fuera de los lados del triángulo.
da
soluciones fuera de los lados del triángulo.
Si se resuelve el sistema formado por estas dos ecuaciones en c y d, se obtiene
![]() .
.