Problema 133.- Dividir un triángulo en dos figuras, un cuadrilátero y un triángulo de la misma área por un punto que no sea vértice ni punto medio de un lado. Barroso, R. (2004) Comunicación personal.
Solución del profesor Saturnino Campo Ruiz. IES Fray Luis de León. Salamanca.-
Para el área del triángulo, si llamamos b’ y h’ a su base y su altura, se ha de verificar que b’h’= ½· bh siendo b y h base y altura de ABC.
 Si queremos que los puntos que dividan al
triángulo estén comprendidos entre los vértices, la altura h’ será
menor que h, y en consecuencia, b’ será mayor que b/2.
Para hacer la construcción usaremos las propiedades de la potencia de un punto
respecto a una circunferencia.
Si queremos que los puntos que dividan al
triángulo estén comprendidos entre los vértices, la altura h’ será
menor que h, y en consecuencia, b’ será mayor que b/2.
Para hacer la construcción usaremos las propiedades de la potencia de un punto
respecto a una circunferencia.
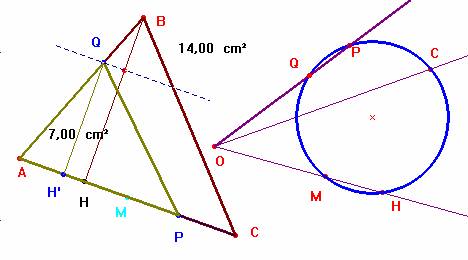
En la una semirrecta de origen un punto O, llevamos los segmentos OM = AM=½. AB y OH=BH (altura sobre b). En otra semirrecta llevo el segmento OC= AC. Construyo la circunferencia que pasa por M, H y C. (Si el punto M coincide con H, la mediatriz del segmento se sustituye por la perpendicular a la semirrecta en ese punto). Si tomo el punto P sobre MC (así AP será mayor que b/2) una circunferencia de centro O con radio AP corta a la anterior en el punto P. La semirrecta OP determina el punto Q, de forma que h’= OQ sea la altura del triángulo de base AP y área la mitad la de ABC. Para determinar Q en el triángulo se lleva sobre la altura, a partir de H el segmento h’. Una paralela a la base por el extremo del mismo nos determina el punto Q deseado. El cuadrilátero PQBC tiene área la mitad de ABC. c.q.d.