Problema 134.-
Dividir un triángulo en dos figuras, un cuadrilátero y un triángulo del mismo perímetro por un segmento que pase por un punto que no sea un vértice.
Barroso, R. (2004) Comunicación personal

Solución de F. Damián Aranda Ballesteros

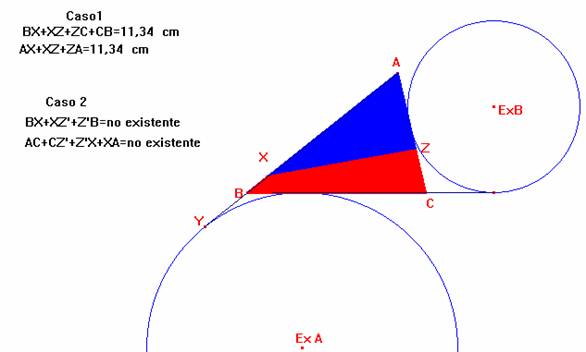
Supongamos que el punto X varía sobre el lado AB=c.

Contemplamos dos casos:

Caso 1- AX > s-b

Analizando la figura a construir ha de suceder que:
AX+XZ+AZ = XZ +ZC +CB +BX = XZ + (b-AZ) + a + (c-AX)

En definitiva:
2×(AX+AZ) = a + b + c;         AX + AZ = (a+b+c)/2 = s

Luego se ha de verificar que la suma AX + AZ = s.

Ahora bien, como AZ ha de ser menor o igual que el lado AC= b, la relación sí será válida  en este caso ya que: AX = s - AZ > s - b.

Caso 2- AX < s-b

Si tenemos por el contrario que AX < s-b, la situación será la siguiente:

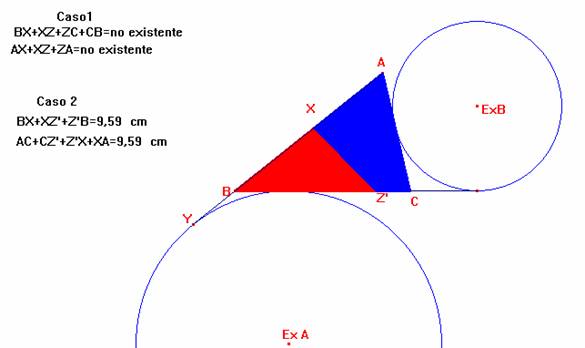
Analizando la figura a construir ha de suceder que:
BX+XZ’+BZ’ = XZ’ +Z’C +CA +AX = XZ’ + (a-BZ’) + b + (c-BX)

En definitiva:
2×(BX+BZ’) = a + b + c;        BX + BZ’ = (a+b+c)/2 = s

Luego se ha de verificar que la suma BX + BZ’ = s.

Ahora bien, como BZ’ ha de ser menor o igual que el lado BC= a, la relación anterior será válida ya que: BX = s - BZ’ < s - a.

Pero esta desigualdad es cierta pues    BX= c-AX  y   AX<s-b,  luego entonces:
c+b-s < c-AX = BX

y como c+b-s = s-a, tenemos que, en efecto:  s-a < BX,       c.q.d.