Sofisma tercero. Demostrar que todos los triángulos son isósceles. Sea ABC un triángulo cualquiera. Tomemos el punto medio D del lado BC considerándolo como base, y tomemos por D la perpendicular a BC: Tracemos ahora la bisectriz del ángulo opuesto A.

1º.- Si esta bisectriz no se encuentra a la perpendicular a BC por D, siendo por tanto paralela a ella y, por consiguiente, es perpendicular a BC, en ese caso el triángulo ABC es isósceles.

2º.- Si la bisectriz del ángulo se encuentra con la perpendicular a BC por D, el punto de encuentro O está en el interior o en el exterior del triángulo.

Supongamos en primer lugar que está en el interior, desde este punto O, tracemos las perpendiculares OE, y OF sobre AC y BC, y después tracemos OB y OC.

El punto O está en la bisectriz del ángulo A, por lo que las dos perpendiculares OE y OF sin iguales y los dos triángulos rectángulos OAE y OAF son iguales, por lo tanto (I) AE=AF. De igual manera OB=OC, y los dos triángulos rectángulos OCE y PBF son también iguales, de donde: (II) EC=BF. Sumando miembro a miembro (I) y (II), tenemos: AE+EC=AF+BF de donde AC=AB, de donde se tiene la conclusión de que el triángulo ABC es isósceles.

Supongamos en segundo lugar que el punto O esté en el exterior del triángulo ABC. Hagamos la misma construcción: Los dos triángulos rectángulos OAE, OAF son iguales y (1) AE=AF. Del mismo modo, la igualdad de los dos triángulos rectángulos OCE, OBF nos da (2) CE=BF.

Restando miembro a miembro (1) de (2), queda: AE-CR=AF-BF, de donde AC=BC.

Así pues, el triángulo ABC es isósceles en todos los casos posibles, resultado evidentemente absurdo.

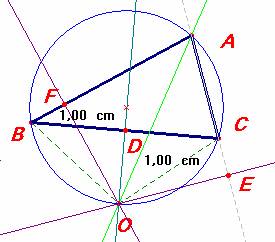Solución del profesor Saturnino Campo Ruiz. IES Fray Luis de León. Salamanca.-

El punto O donde concurren la mediatriz de un lado con la bisectriz del ángulo opuesto está sobre la circunferencia circunscrita, (ver problema nº 32) debido a ello el ángulo BOC es suplementario del ángulo en A, y también el FOE por ser rectos los ángulos en F y en E. En consecuencia, estos ángulos son iguales entre sí, de ahí que si el punto F es interior al lado AB, el punto E corta a AC en su prolongación (o viceversa), de manera que siendo ciertas las igualdades AE = AF; CE = BF, AE – CE = AC no es igual a AF + BF = AB, con lo que se prueba la falsedad del sofisma.