Problema 137
Sea ABC un triángulo. Sea P un punto que no pertenezca al mismo. Trazar por P una recta de manera que corte al triángulo en dos figuras geométricas de la misma área.

Propuesto por José Nogareda Villar, profesor de matemáticas del IES "Ramón Olleros de Béjar" (Salamanca).

Solución de F. Damián Aranda Ballesteros

Para evitar casos triviales, supondremos que el punto P es exterior y no pertenece a ninguna mediana del triángulo. Tampoco pertenece a ningún lado de algún triángulo semejante al inicial y de razón .
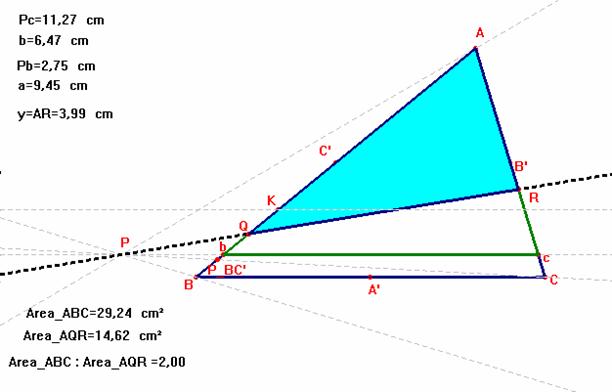
Lanzamos semirrectas con origen el punto P hacia cada uno de los vértices A, B y C del triángulo inicial. Estas semirrectas determinarán siempre un punto de intersección en alguno de los seis segmentos BC’, C’A, AB’, B’C, CA’ y A’B. En nuestro caso y para posicionarnos sea el caso en que la recta PC corta al segmento BC’ en el punto P­_BC’. Sea K el punto situado en el lado BA tal que AK= ∙AB.
Si la paralela por el punto P al lado BC, recta bc,  queda por debajo (encima) de la paralela al lado BC por K, como es nuestro caso, entonces la recta deseada ha de estar comprendida entre las dos. De esta manera, la recta solución de nuestro problema cortará al triángulo Abc en los puntos P, Q y R y se dará, por tanto, la relación de Menelao entre los segmentos interceptados. Es decir:

Sean los segmentos AQ = x , AR = y, entonces (1) se podrá expresar, una vez desarrollada aquella expresión, como:           

Como, por otro lado, para que se de la relación entre las áreas de los triángulos ABC y AQR, una el doble de la otra, tendrá que ser x∙y = ½∙ b∙c (2)

Resolviendo el sistema que proporcionan las ecuaciones (1) y (2), obtenemos:

, cuya solución positiva será la válida para AR=y:

Uniendo P con R determinamos el punto Q y así el triángulo AQR demandado.

Nota 1:
Que el resultado implique una ecuación de segundo grado, prueba que el problema tiene solución con regla y compás.

Nota 2:

En las demás situaciones posibles del punto P, se actuaría de un modo similar al expuesto sin más que tener en cuenta los nuevos considerandos particulares.