Propuesto por José Nogareda Villar, profesor de matemáticas del IES "Ramón Olleros de Béjar" (Salamanca).
PROBLEMA 137: Sea ABC un triángulo. Sea P un punto que no pertenezca al mismo. Trazar por P una recta de manera que corte al triángulo en dos figuras geométricas de la misma área. Nogereda, J. (2004): Comunicación personal
Solución de José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona) (10 de febrero de 2004)
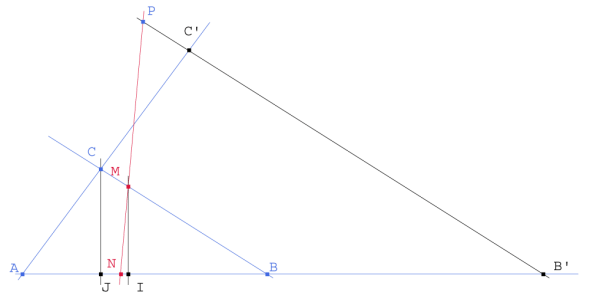 Figura 1
Figura 1
Si PM es la solución, el área del triángulo MNB es igual al área del polígono MNAC.
Enunciado
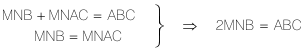
Igualdad de áreas
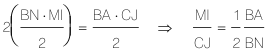
Triángulos semejantes (AJB, MIB)

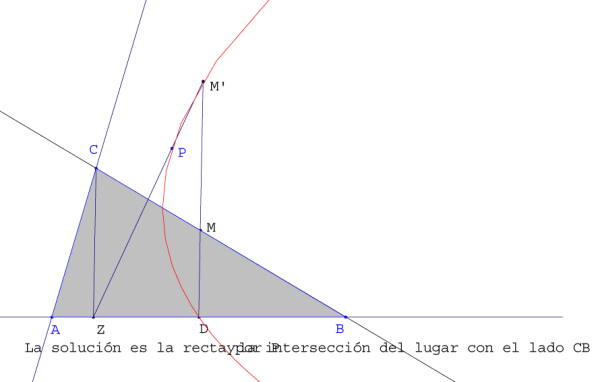 Figura 2
Figura 2 Vamos a prescindir de P. Si M fuera la solución
 .
.
Tomamos sobre BC un punto M que unimos con D, punto medio de BA. Paralela por C a MD y corta BA en Z .
Unimos Z con P. Si Z fuera la solución MD y PZ se cortarían en M; pero en general se cortan en un punto M’.
Basta pues buscar el lugar geométrico de M’ cuando desplazamos M sobre BC.
La intersección de ese lugar con BC nos da la solución.
Si trabajamos con Cabri II plus, hemos finalizado. Cabri II plus realiza la intersección de distintos objetos geométricos, incluídos los lugares geométricos).
Si trabajamos con cabri II tradicional, esto no es posible, debemos crear el lugar construyendo por puntos.
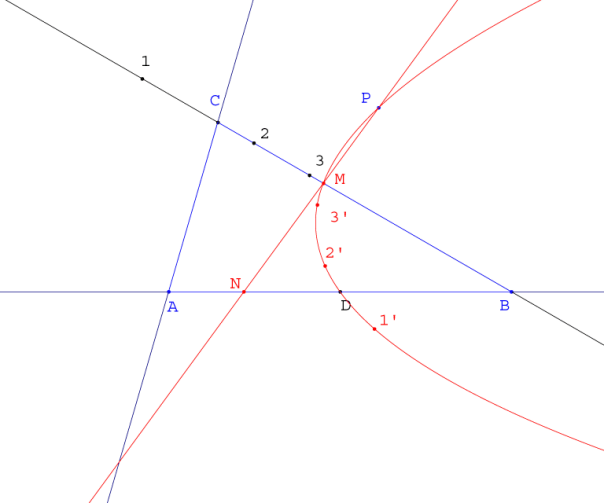 Figura 3
Figura 3 Cabri II permite la construcción de una cónica por cinco puntos; pero sólo necesitamos tres.
El punto dado P pertenece al lugar, ya que éste está generado por una recta por P.
El punto medio de BA también es del lugar, ya que si M coincide con C entonces Z=D=M’.
Para el resto de puntos (1,2,3) realizamos la construcción de la página anterior y obtenemos (1', 2', 3'). Abrimos el menú de cabri, cónica por cinco puntos (1', 2', 3' D, P) y ya hemos terminado
nota
Para obtener puntos, tenemos una macro (137lugar.mac):
Elegimos el triángulo, el punto P y un punto cualquiera sobre BC