Propuesto por José Nogareda Villar, profesor de matemáticas del IES "Ramón Olleros de Béjar" (Salamanca). PROBLEMA 137: Sea ABC un triángulo. Sea P un punto que no pertenezca al mismo. Trazar por P una recta de manera que corte al triángulo en dos figuras geométricas de la misma área. Nogereda, J. (2004): Comunicación personal Solución de José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona) (12 de febrero de 2004)
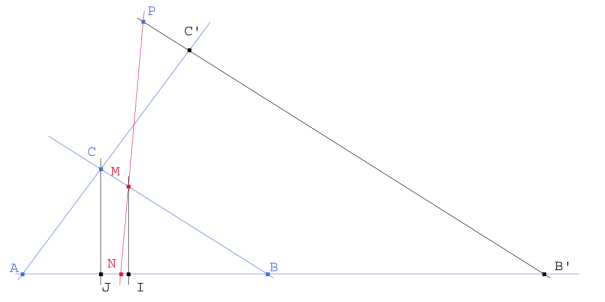Figura 1
Si PM es la solución, el área del triángulo MNB es igual al área del polígono MNAC.
Enunciado
Igualdad de áreas
Triángulos semejantes (AJB, MIB)
Triángulos semejantes (MNB, PNB’)
Poniendo todo junto
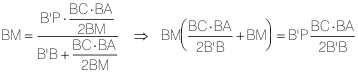
Acabamos de transformar el problema original en este nuevo problema:
Dados dos segmentos a y b, encontrar el segmento x tal que:
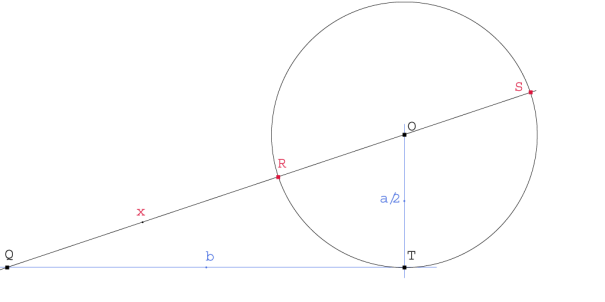Figura 2
Para resolverlo, recordamos las propiedades de la potencia de un punto respecto a un círculo. Vemos que hay dos soluciones
Resolución y construcción del nuevo problema Sea el segmento QT de longitud b. Sobre la perpendicular por T, llevamos TO de longitud a/2. Trazamos el círculo de centro O y radio a/2 tangente a PT en T. La intersección de QO con el círculo, da dos soluciones QR y QS.
En nuestro caso
Vuelta al problema original Obtenido x determinamos BM. La recta PM es la solución.
CONSTRUCCION
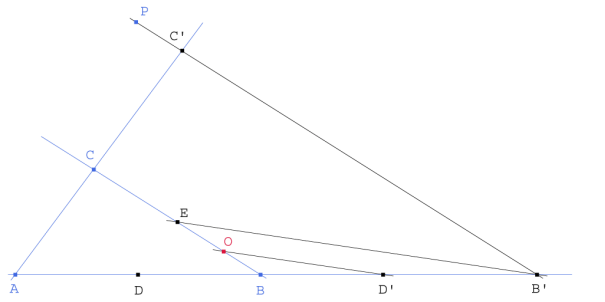Figura 3
Trazamos, por P, una paralela a BC. Esta corta a BA en B` y en Ć a CA. Hallamos 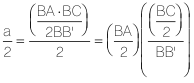. Para , unimos E, punto medio de BC con B́, para multiplicar por llevamos por D́, simétrico del punto medio de AB respecto a B. una paralela a B́E que corta a BC en O, Entonces .


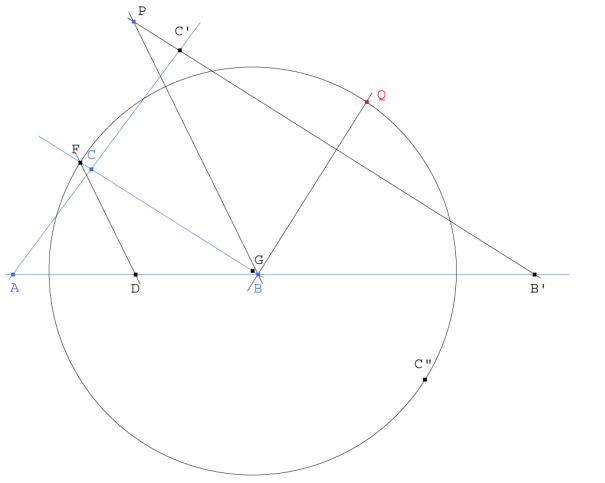
Hallamos Para , unimos B con P. Para multiplicar por , por punto medio de BA, paralela a BP que corta a BC en F. Entonces y así . Para b, trazamos el círculo de diámetro (Ć́ simétrico de C respecto a B). La perpendicular por B a FĆ́ nos da Q sobre el círculo trazado, tal que .
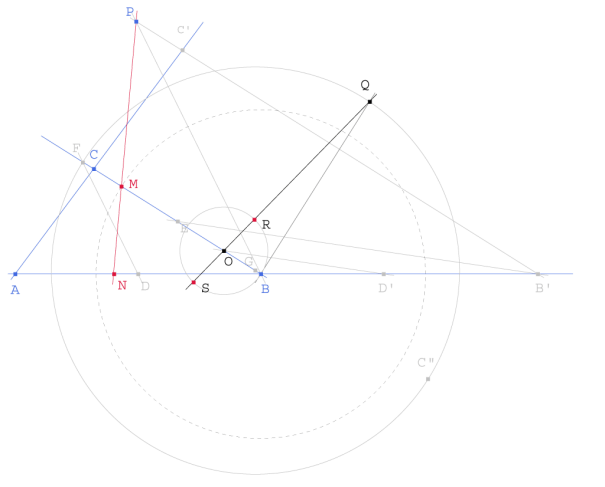
Trazamos ahora la recta QB que corta al círculo en R y S. Tomamos la solución QR y llevamos . M es el punto buscado. La recta PM es la solución buscada.