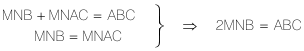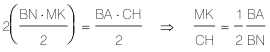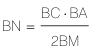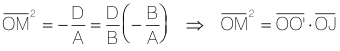Propuesto por José Nogareda Villar, profesor de matemáticas del IES "Ramón Olleros de Béjar" (Salamanca). PROBLEMA 137: Sea ABC un triángulo. Sea P un punto que no pertenezca al mismo. Trazar por P una recta de manera que corte al triángulo en dos figuras geométricas de la misma área. Nogereda, J. (2004): Comunicación personal Solución de José María Pedret. Ingeniero Naval. Esplugas. 19 de febrero de 2004 |
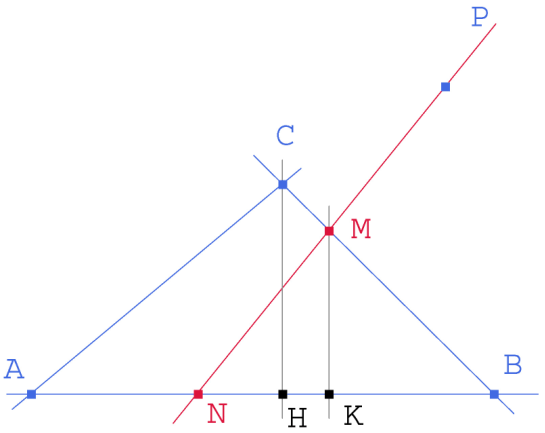 Figura 1 Figura 1
|
Si PM es la solución, el área del triángulo MNB es igual al área del polígono MNAC. |
Enunciado
|
Igualdad de áreas
|
Triángulos semejantes (CHB, MKB)
|
Vamos a prescindir de P. Si M fuera la solución
|
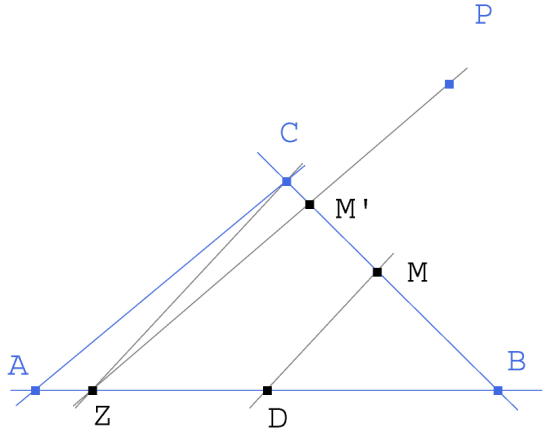 Figura 2 Figura 2
|
Tomamos sobre BC un punto M que unimos con D, punto medio de BA. Paralela por C a MD y corta BA en Z . Unimos Z con P. Si Z fuera la solución MD y PZ se cortarían en M; pero en general PZ corta a BC en un punto M’. M’ es la imagen de M por una homografía de la recta BC sobre sí misma. Si la solución exige la coincidencia de M con M’, significa que el punto solución es un punto doble de la homografía.
|
|
Dada una homografía de una recta sobre sí misma, hallar los puntos dobles. |
Para hallar los puntos dobles, usaremos los puntos límite y un sistema de referencia: |
Puntos límite son los homólogos de los puntos del infinito:
El sistema de referencia es la recta, con origen O, el punto medio de los puntos límite. Puntos dobles (método 1) Sabemos que la relación algebraica que define la homografía es de la forma:
donde x y x’ son las abscisas de un punto de la recta y su homólogo, en la homografía.
y como tomamos como origen el punto medio de los dos
Quedando la ecuación de la homografía como
Para los puntos dobles M
La imagen O’ del origen O es
y poniéndolo todo junto
Igualdad que nos permite construir los puntos dobles M. |
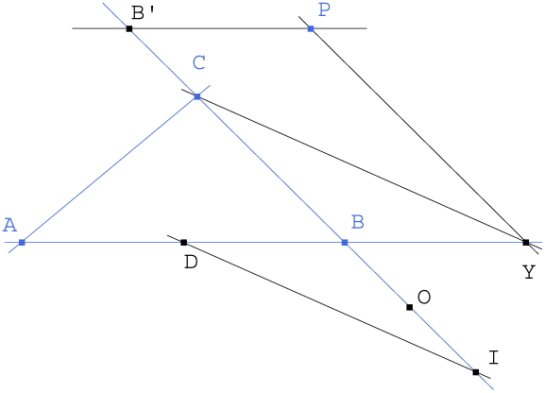 Figura 3 Figura 3
|
Para nuestro problema, h(I)=∞ y h(∞)=B. Para hallar I trazamos por P, paralela a BC (dirección infinito), corta a BA en Y, unimos Y con C y para lela por D, punto medio de BC, corta a BC en I. (No es más que la construcción inversa) h-1(∞)=I.
No nos hace falta encontrar O’ pues el punto medio entre B y O’ es B’=h(B) y para obtenerlo basta hallar la intersección de una paralela a BA por P y BC. Trazamos la circunferencia de centro en B’ y radio BB’, trazamos la tangente desde O a esta última circunferencia y obtenemos M. Todo junto nos proporciona la siguiente |
CONSTRUCCION (método 1) |
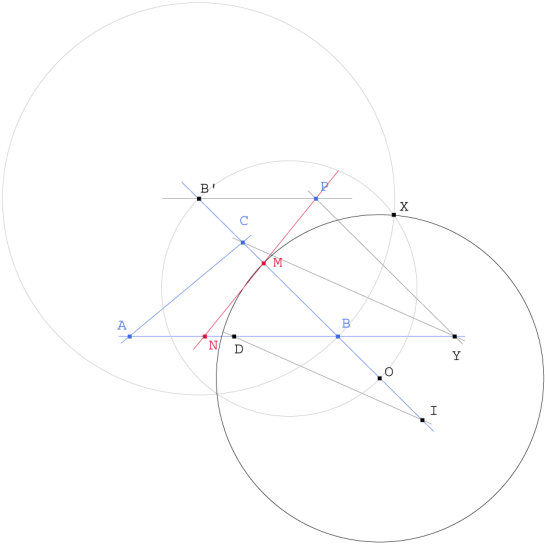 Figura 4 Figura 4
|
a Por P paralela a BC que corta a BA en Y.
b Trazamos la recta YC.
c Por D, punto medio de BA, trazamos paralela a YC que corta a BC en I.
d Por P, paralela a BA que corta a BC en B’.
e Círculo de centro B’ y pasa por B.
f Con O, punto medio de BI. Círculo de diámetro B’O. Corta al último círculo en X
g Con centro en O, círculo que pasa por la intersección X. Su intersección con BC nos da M punto buscado. |
Puntos dobles (método 2) Para algunos, es una pena recurrir a la herramienta algebraica cuando se pueden conseguir los puntos dobles, sin salir del trazado de líneas rectas y circunferencias. |
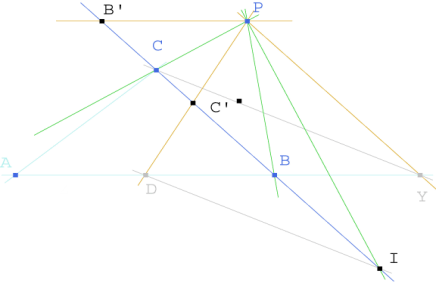 Figura 5 Figura 5
|
En lugar de la homografía de la recta BC sobre sí misma, consideramos los haces de vértice común P que también son homográficos. (P; B, C, I) --->(P; B’, C’,∞ ), con I’=∞. |
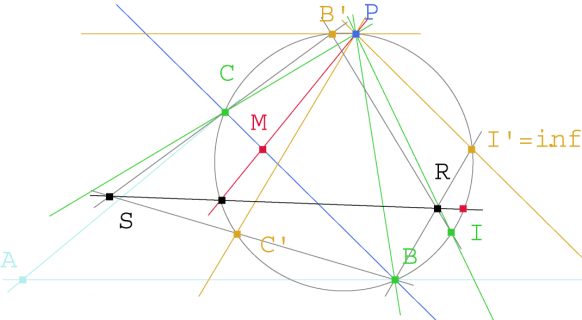 Figura 6 Figura 6
|
cortando dos haces homográficos por un círculo que pase por el vértice común, las intersecciones de los haces y el círculo también son homográficas. Los puntos dobles están en la intersección de ese eje y el círculo.(Distinguimos los puntos sobre el círculo con colores distintos)
Podemos establecer la siguiente |
CONSTRUCCION (método 2) |
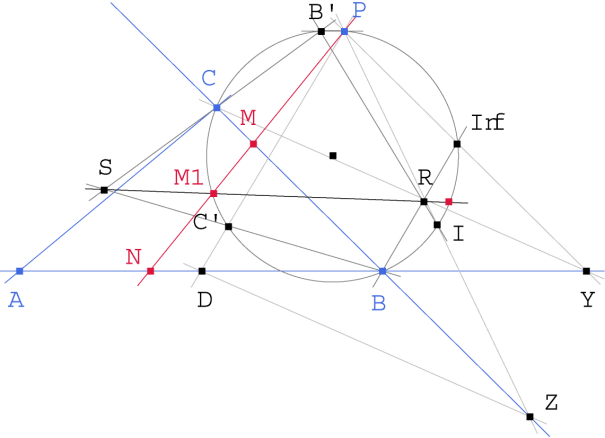 Figura 7 Figura 7
|
PUNTOS HOMOGRAFICOS EN EL CIRCULO a Círculo PBC b Por P, paralela a AB. Corta al círculo en B’ c Por P, paralela a BC. Corta al círculo en I’=Infinito. Corta en Y a AB d Por D, punto medio de AB, recta DP. Corta al círculo en C’ e Por D, paralela a YC. Corta a BC en Z f PZ corta al círculo en I EJE DE LA HOMOGRAFIA RS g R, intersección de B’I con Binf. h S, intersección de BC’ con B’C i RS corta al círculo en M1(punto doble) y M2 j PM1 corta a BC en M y a AB en N pasemos ahora a destacar unos detalles de la construcción Cabri |
CONSTRUCCION CABRI
(1) Lo que nos interesa representar en Cabri es una solución para cualquier punto del plano. La construcción explicada tiene ciertas limitaciones que se ponen de manifiesto al observar como queda dividido el plano por las medianas del triángulo. |
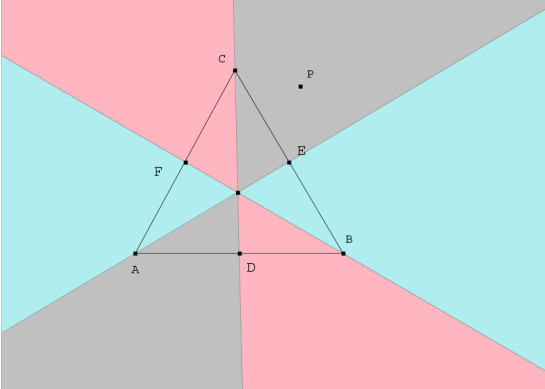 Figura 8 Figura 8
|
Nuestra construcción sólo es válida en la zona gris.
Hemos de repetir la construcción para la zona rosa. Esta construcción es idéntica a la anterior; pero en lugar de considerar el triángulo ABC y P en la zona gris CE, consideramos el triángulo CAB y P situado en la zona rosa BD.
Repetimos la construcción con el triángulo BCA y el punto P en la zona azul AF.
(2) Para las intersecciones basta sustituir el triángulo por segmentos AB, BC y CA.
(3) Hay que construir la solución para M1 y M2.
(4) De la primera construcción sacaremos una macro sólo para obtener M1 y M2 Uniremos P con M1 y/o M2 y trazaremos la solución como la recta que une las intersecciones de PM1 con BC y PM1 con AB (si falta una de las intersecciones, no habrá recta). Trazamos ahora el triángulo y el cuadrilátero de igual área.
(5) De la construcción (1) a (4), sacaremos una macro y la repetiremos dos veces, como hemos dicho más arriba. ( CAB y P) y (BCA y P). [137.mac] |