Problema 137.-Sea ABC un triángulo. Sea P un punto que no pertenezca al mismo. Trazar por P una recta de manera que corte al triángulo en dos figuras geométricas de la misma área.

Propuesto por José Nogareda Villar, profesor de matemáticas del IES "Ramón Olleros de Béjar" (Salamanca). Nogareda, J. (2004): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (16 de febrero de 2004).-

 

 

 

 

 

 

 

 

 

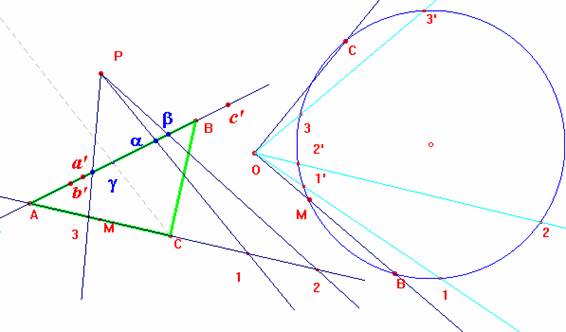
Tomo una recta que pasa por P. Corta al lado AC en un punto X y al lado AB en otro punto Y. Buscamos aquellos puntos X e Y para los cuales  (AXY) = ½· (ABC). Para éstos, la condición sobre el área es  2·(AXY) = AX·AY·senA = ½·AB·AC· senA, es decir, AX·AY =½·· AB·AC  = ½.bc.  mmmmmmmmmmmmmmm

Cada segmento AY sobre AB determina un segmento AX sobre AC de forma que el triángulo AYX tenga como área la mitad de la de ABC. Basta tomar sobre una semirrecta de origen O, segmentos  OM = ½· AC,  OB =AB. En otra semirrecta tomo otro segmento, por ejemplo OC = AB y trazo la circunferencia que pasa por estos tres puntos  M, B y C. Cualquier semirrecta que desde  O la corte, intercepta segmentos cuyo producto es ½ ·bc  y por tanto, permiten construir un segmento XY que divida a nuestro triángulo en dos regiones de igual área.

Fijado un punto sobre AB (o su prolongación), por ejemplo el punto a, la recta que lo une con P define sobre AC el punto 1. Según el método descrito anteriormente puedo determinar otro punto a’  sobre AB que junto con el punto 1 y el  A forme un triángulo de área igual a  ½·( ABC).  (Área de Aa’1 = ½· Área de ABC)

La correspondencia a -->  a’  define una proyectividad sobre la recta AB. Si encontramos sus puntos dobles, habremos encontrado el punto S tal que la recta PS corte al lado AC en R de forma que

(ARS ) =½·· (ABC).

Para determinar los puntos dobles de la proyectividad sobre la recta AB definida por

(a, b, g)  à (a’, b’, c’)

proyectamos esta recta sobre una circunferencia cualquiera desde un punto V de la misma (no perteneciente a AB), como polo de proyección. Hallamos los puntos dobles de la aplicación inducida en la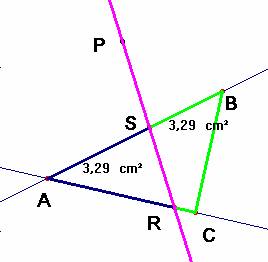

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

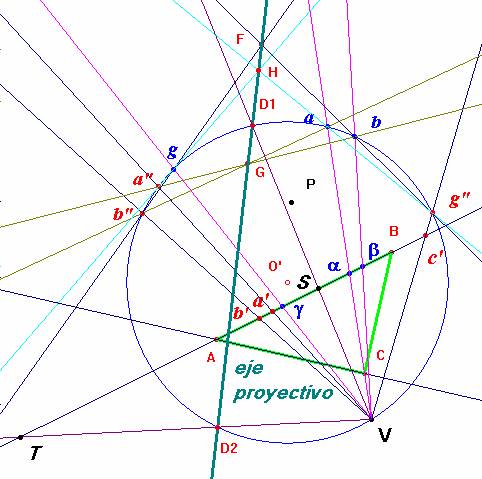
circunferencia como ya explicamos al tratar el problema de Castillon (ver problema número  82 ).  La aplicación inducida está definida por (a, b, g) à (a”, b”, g”) . Los puntos de intersección de ab” con a”b;  de ag” con a”g y de bg” con b”g están alineados en la recta eje proyectivo. El corte de esta recta con la circunferencia da los puntos dobles D₁ y D₂,  de la aplicación. Su proyección sobre AB crea los puntos fijos buscados en esta recta, S y T y la solución al problema. En nuestro caso S es el punto doble que junto con R y A dan el triángulo pedido.(El punto T es exterior al segmento AB y no sirve). Por último, desde el punto P,  uniendo con S hallamos sobre AC el punto R. El triángulo ASR y el cuadrilátero  SRBC tienen igual área como deseábamos hallar.