Problema 137.-Sea ABC un triángulo. Sea P un punto que no pertenezca al mismo. Trazar por P una recta de manera que corte al triángulo en dos figuras geométricas de la misma área.
Propuesto por José Nogareda Villar, profesor de matemáticas del IES "Ramón Olleros de Béjar" (Salamanca). Nogareda, J. (2004): Comunicación personal.
Solución euclídea del profesor Saturnino Campo Ruiz, IES Fary Lius de León de Salamanca (2 de marzo de 2004).- 1º.- Veamos como expresar la condición sobre las áreas.
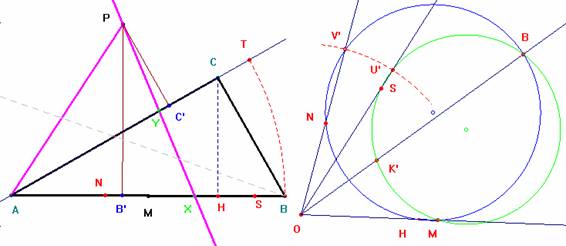
Trazamos desde P una recta que corta en Y al lado AC y en X al lado AB. El área del triángulo APX es la suma de las áreas de los triángulos APY y AYX. La de este último ha de ser igual a la mitad del área de ABC. Tendremos así la relación:
2(AYX) = (ABC) = 2(APX) — 2(APY) = AX·PB’— AY·PC’. (1)
Si represento el área de ABC como el producto de dos segmentos, uno de ellos, la altura de uno de estos triángulos, por ejemplo, PB’; el otro segmento lo calculamos tomando una semirrecta de origen O, sobre la que llevamos OH =CH (altura); OM =1/2·AB (base). En otra semirrecta llevamos, por ejemplo, la base AB determinando el segmento OB. El círculo que pasa por estos puntos (de color azul) es tal que cualquier semirrecta que lo corte intercepta segmentos cuyo producto es igual al área del triángulo ABC. De este modo, tomando OV’ = PB’, hallamos el punto N, tal que ON·OV’ =AN·PB’ = (ABC). Volviendo a (1), sustituyo (ABC) y resulta
AN·PB’= AX·PB’— AY·PC’, de donde, (AX—AN)·PB’ =AY·PC’,
NX·PB’ = AY·PC’ ó ![]() (2)
(2)
Los puntos X e Y que buscamos para que el triángulo AYX tenga como área la mitad de la del triángulo ABC son aquellos puntos cuya razón de distancias a dos puntos determinados A y N es conocida (dada por el cociente de otros dos segmentos).
2º.- Evidentemente, hay infinitos puntos que cumplen estas condiciones. La ecuación (2) define una correspondencia entre los puntos de la recta AB y los puntos de la recta AC. Una solución particular trivial es X=N, Y=A. Si X=S, Y=T es otra solución, podemos extender esta correspondencia a todo el plano sin más que considerar la semejanza directa que transforma el vector NS en el AT. El centro Q de esta semejanza va a ayudarnos a hallar el par (X,Y) solución de (2) que está alineado con P, pero antes vamos a hallar una segunda solución (S,T).
Fijando AY = AB, calculo X=S como sigue: tomo OK’ = PC’; OB = AB y OU’ = OV’. De este modo la semirrecta OU’ corta a la circunferencia que pasa por K’ , M y B (de color verde) en el punto S buscado. Llevo este segmento sobre el lado AB, OS = NS y ya está sobre el triángulo ABC una solución particular de la ecuación (2): los puntos X =S e Y=T que, como era de esperar, no están alineados con P.
3º.-
 Si
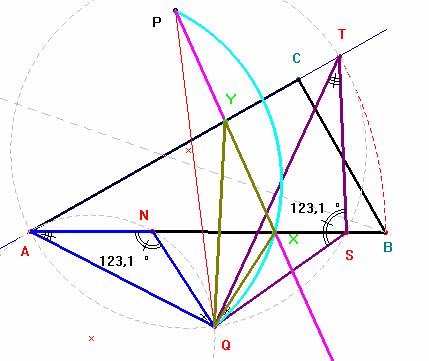
Q es el centro de la semejanza, los triángulos NQS y AQT
son semejantes; de la igualdad de los ángulos en Q, restando a
ambos el ángulo NQT obtenemos <TQS =<AQN y de
ahí la semejanza de los triángulos QST y QNA (pues tienen un
ángulo igual y los lados proporcionales).
Si
Q es el centro de la semejanza, los triángulos NQS y AQT
son semejantes; de la igualdad de los ángulos en Q, restando a
ambos el ángulo NQT obtenemos <TQS =<AQN y de
ahí la semejanza de los triángulos QST y QNA (pues tienen un
ángulo igual y los lados proporcionales).
Para la solución (X,Y) alineada con P se tiene la misma relación: el triángulo XQY es semejante al NQA, así pues, el punto X pertenece al arco capaz de QP y amplitud el ángulo <QST= <QNA; además, pertenece al lado AB. El arco capaz y su corte con el lado AB nos da X.
4º.- Para hallar el centro de la semejanza que transforma NS en AT (ver problema nº 91) hallamos el punto de intersección de las circunferencias que pasan por cada par de homólogos (N y A; S y T) y su intersección. En este caso el punto de intersección es el punto A, así pues hallaremos la circunferencia que pasa por A, T y S y la circunferencia que pasa por A, N y es tangente a AT en A.