Propuesto por Francisco Javier García Capitán, (Bella Geometría) profesor del IES Álvarez Cubero (Priego de Córdoba)
Problema 138: Dado un triángulo ABC trazar una secante que corte a AB en M y a BC en N, de manera que el cuadrilátero AMNC y el triángulo BMN tengan el mismo perímetro y la misma área. Preparación de Olimpíadas.
Solución de José María Pedret. Ingeniero naval. (Esplugas de Llobregat, Barcelona), 3 de febrero de 2004
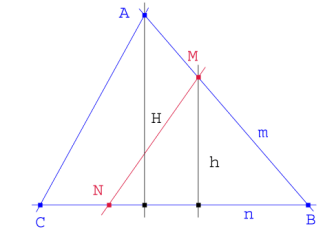
Igualdad de áreas:
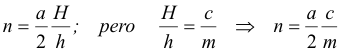
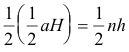
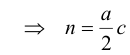
Igualdad de perímetros:
El problema se ha convertido en buscar dos segmentos m y n cuya suma y producto son conocidos.
Problema conocido; pero adecuamos la solución a la configuración de nuestro problema,
realizamos la solución encima de nuestra figura, sacando ventaja de ella y economizando construcciones.
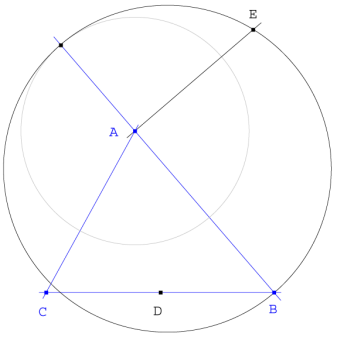
Llevamos, a partir de
,
, sobre
y trazamos el círculo de diámetro
.
Perpendicular a
por
, que corta al círculo anterior en E, y así:
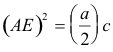
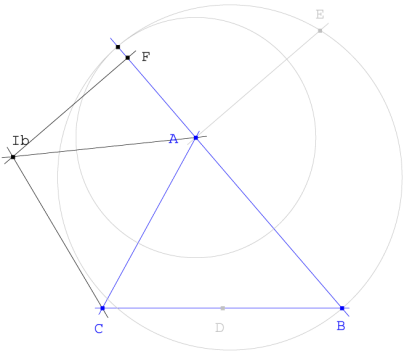
Con el punto de contacto del círculo ex-inscrito opuesto a B determinamos
tal que
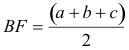
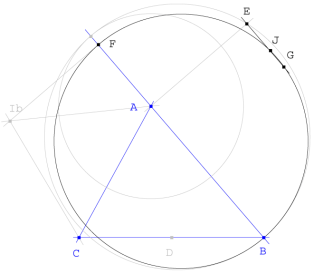
Trazamos el círculo de diámetro
, la paralela a
por
corta a este último en
y
.(2 soluciones). Las perpendiculares a
por
y
dan
y
sobre
.
Los dos segmentos están en la posición necesaria para acabar el problema original:
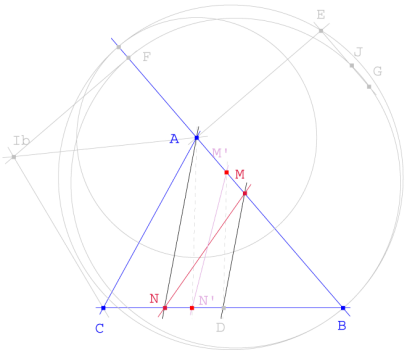
Tenemos
y sabemos que:
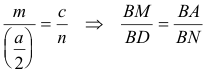por tanto, la paralela por
a
nos proporciona
en su intersección con
. Análogamente, obtenemos
, la
segunda solución.