Problema 138.-Dado un triángulo ABC trazar una secante que corte a AB en Q y a AC en P, de manera que el cuadrilátero BQPC y el triángulo AQP  tengan el mismo perímetro y la misma área. Propuesto por Francisco Javier García Capitán, (Bella Geometría) profesor del IES Álvarez Cubero (Priego de Córdoba)

 Solución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (10 de febrero de 2004).-

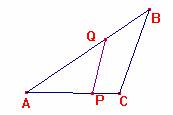Para dividir el triángulo ABC en dos figuras de igual área procederemos como sigue:

                Si es APQ el triángulo cuya área es la mitad de la de ABC se verifica que:

 2 = , esto es,  AP·AQ =bc/2  (1)

 Si además imponemos la condición de la igualdad de los perímetros de las dos figuras,  se ha de verificar AP + AQ = p   (2), donde p es el semiperímetro de ABC.

En resumen: tenemos que construir dos segmentos AP  y AQ cuya suma y cuyo producto son dados.

Las longitudes de estos segmentos son las soluciones de la ecuación de segundo grado

x²- px + bc/2 = 0      (3)

Resolviendo obtenemos                             (4)

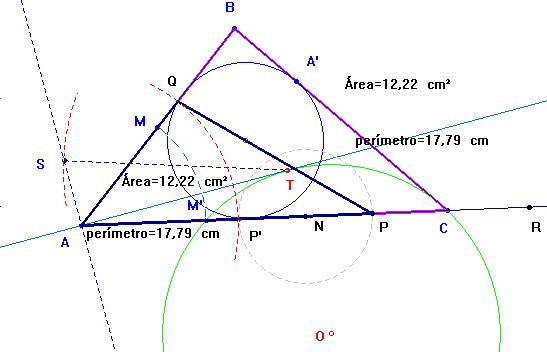
Veamos cómo construimos geométricamente estas soluciones. Si sabemos construir la raíz cuadrada de bc/2 tendremos también la raíz de la expresión (4), pues, según el teorema de Pitágoras, se trata del cateto que completa un triángulo rectángulo de hipotenusa p/2 y cateto igual a la raiz cuadrada de bc/2.

Comencemos con ésta última. Tomo M el punto medio de AB y lo llevo a M’ sobre AC. Se traza una circunferencia cualquiera que pase por M' y  C de centro O. La tangente a ella desde A nos determina el punto T con la propiedad de AT·AT = bc/2.

                Para la raíz de (4) comenzamos calculando el segmento de longitud p/2. El punto A’ de contacto de la circunferencia inscrita en ABC,  determina el segmento BA’ = CR = p-b. Por tanto, AR = p. Si N es su punto medio, tengo ya AN = p/2. Trazo una perpendicular a AT por A y con radio p/2 desde T trazo un arco que corta en S a la misma. He hallado el valor de la raíz cuadrada que figura en la expresión (4),  AS. Con centro N y radio AS trazo un círculo que corta en P  y en P’ al lado AC. Los segmentos AP y AP’ son las soluciones de la ecuación (3). Llevando AP’ sobre AB determinamos el punto Q, que junto con P resuelven el problema.