Problema 140
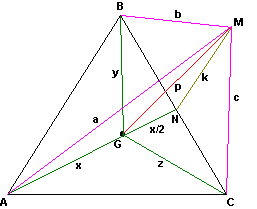
Sea G el baricentro del triángulo.Sea M un punto cualquiera del plano.
Entonces, MA MA + MB MB + MC MC = AG AG + BG BG + CG CG + 3 MG MG
Rouché - Comberousse. (1929): Traité de Géomètrie. Gautier- Villars. París (pág 393)
En catalán
Problem
Siga G el baricentre del triangle . Siga M un punt qualsevol del plànol.
Aleshores: MA MA+MB MB+ MC MC = AG AG + BG BG + CG CG + 3 MG MG
Rouché-Comberousse (1929).Traité de Géométrie Gauthier-Villars ed. Paris. 1929. p 393.
Solución del profesor William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (4 de febrero de 2004)
En el triángulo AMN: aplicamos el teorema de la ceviana.
![]()
Ahora en el triángulo BGC: aplicamos el teorema de la mediana.
![]()
Siendo “l” la medida del lado BC del triángulo
Y por ultimo en el triángulo BMC: aplicamos también el teorema de la mediana.
![]()
Sumando las tres ecuaciones obtenemos:
![]()
lqqd