Problema 141

Propuesto por Francisco Javier García Capitán, profesor del IES Álvarez Cubero (Priego de Córdoba)

Proyectamos los vértices de un triángulo ABC sobre los puntos A', B', C' de una recta m cualquiera del plano de ABC. Trazamos las rectas A'A" , B'B" , C'C" perpendiculares a BC, CA y AB , respectivamente. Entonces:

a Las tres rectas se cortan en un punto M . (J. Neuberg)

F.G.M (1912): Exercices de géométrie,... 5ª edición (pág. 632)

Solución de José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona) (30 de marzo de 2004)

a)

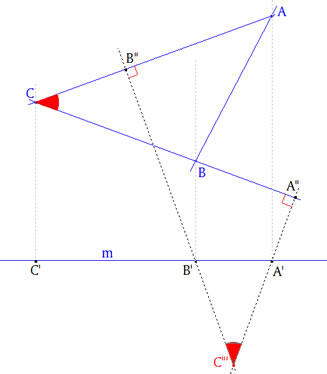
Por proyección (ortogonal) sobre m de los vértices del triángulo, obtenemos A’, B’, C’.

Determinamos A” y B” según el enunciado.

Sea C’” = A’A” ∩ B’B” ; por construcción (perpendicularidad) ∠A’C’”B’ = ∠ACB, entonces podemos decir que C está en el arco capaza de cuerda A’B’ y ángulo ACB. O también que C”’ está en el lugar geométrico de los puntos desde donde se ve A’B’ bajo un ángulo C.

Y así, si A’” = B’B” ∩ C’C”, A’” está en el arco capaz de cuerda B’C’ y ángulo CAB.

Los dos arcos anteriores se cortan en dos puntos, uno de ellos es B’ el otro es el punto M buscado ya que cumple con las dos propiedades de C’” y A’”.

b)

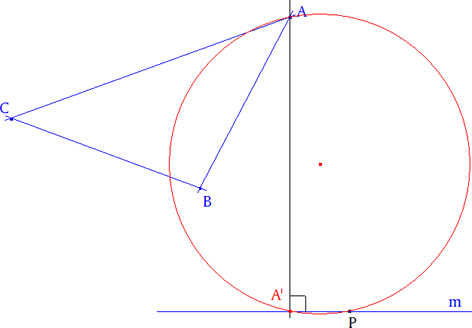
PRIMERA CUESTION PREVIA

Sea m una recta por O, circuncentro de ABC. ¿Cuál es el lugar geométrico de la proyección A’ de A sobre m si m gira en torno a O?

De forma general, hagamos girar m respecto a uno de sus puntos P. El lugar pedido es el del vértice A’ de un ángulo recto cuyos catetos pasan por dos puntos fijos A y P. El lugar pedido es el círculo de diámetro AP.

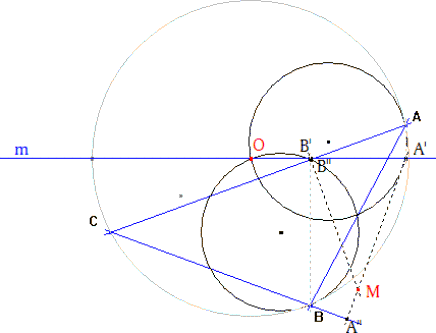
En particular, si m pasa por O y P = O tenemos:

A’ describe la circunferencia de diámetro OA.

B’ describe la circunferencia de diámetro OB.

C’ describe la circunferencia de diámetro OC.

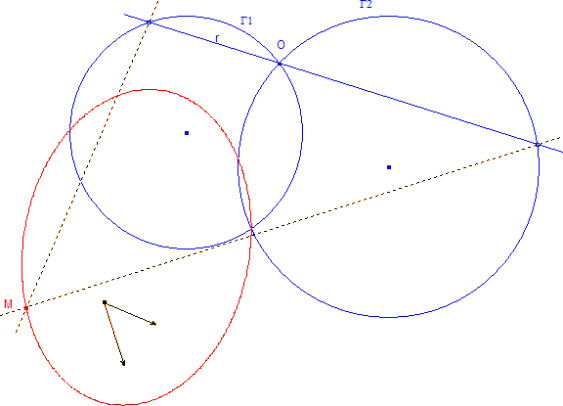
SEGUNDA CUESTION PREVIA

Vista la figura anterior, ¿Cuál es el lugar geométrico del punto M cuando la recta m gira en torno a O? Observemos la figura siguiente:

En general:

-dados dos círculos Γ1, Γ2 que se cortan,

-dada una recta r que gira entorno a uno de los puntos de intersección O,

-dadas dos rectas que se mantienen perpendiculares a dos direcciones fijas (los dos vectores) y

pasan por los otros puntos de intersección de la recta r y los dos círculos Γ1, Γ2

El lugar geométrico del punto M de intersección de las dos rectas ES UNA CONICA que pasa por el otro punto de intersección de los dos círculos.

Volviendo ahora al problema original, determinaremos cinco puntos de esa cónica.

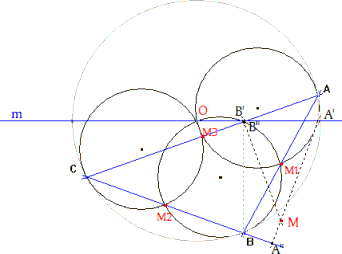
Los tres círculos cortan en O. Si la cónica buscada debe pasar por los otros puntos de intersección de los círculos, pasará por los puntos M1, M2 y M3. Que a su vez son los puntos medios de los lados del triángulo

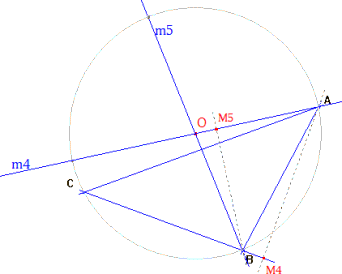
Si m = OA entonces A=A’ y M es el pie de la altura por A. Obtenemos M4.

Análogamente obtenemos M5 cuando B=B’. M5 es el pie de la altura por B.

Ahora bien, si la cónica pasa por cinco puntos, los tres puntos medios de los lados del triángulo y los pies de las alturas del triángulo; y sabemos que estos puntos a su vez están sobre el círculo de nueve puntos. Como la cónica por cinco puntos es única, esa cónica es dicho círculo y por tanto hemos demostrado que M ESTÁ SOBRE EL CÍRCULO DE NUEVE PUNTOS.
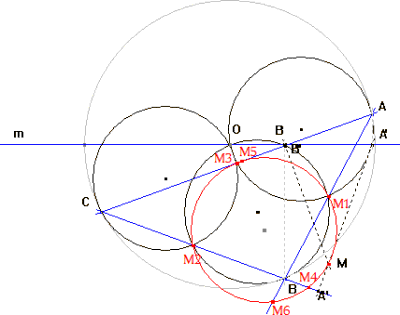