Problema 141

Proyectamos los vértices de un triángulo ABC sobre los puntos A', B', C' de una recta m cualquiera del plano de ABC. Trazamos las rectas A'A" , B'B" , C'C" perpendiculares a BC, CA y AB , respectivamente. Entonces:

a Las tres rectas se cortan en un punto M . (J. Neuberg)

b Cuando la recta m pasa por el centro O de la circunferencia ABC , el punto M está sobre la circunferencia de los nueve puntos de ABC . (Soons, profesor en Tirlemont) Se

F.G.M (1912): Exercices de géométrie,... 5ª edición (pág. 632)

PRIMERA PARTE

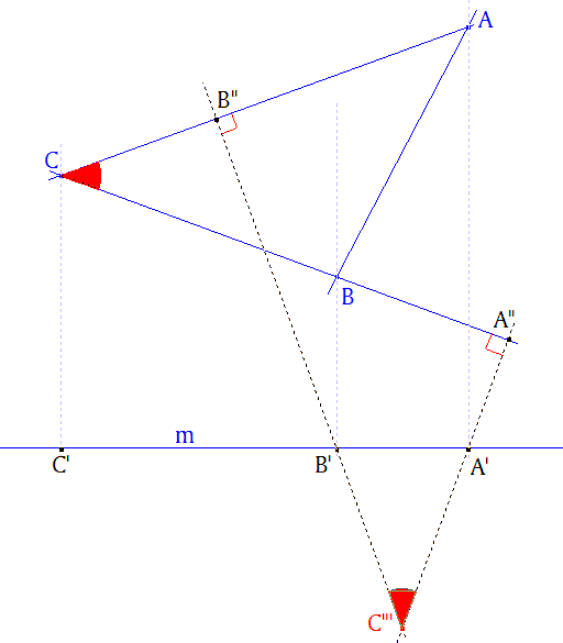
Por proyección (ortogonal) sobre m de los vértices del triángulo, obtenemos A’, B’, C’.

Determinamos A” y B” según el enunciado.

Sea C’” = A’A” ∩ B’B” ; por construcción (perpendicularidad) ∠A’C’”B’ = ∠ACB, entonces podemos decir que C está en el arco capaza de cuerda A’B’ y ángulo ACB. O también que C”’ está en el lugar geométrico de los puntos desde donde se ve A’B’ bajo un ángulo C.

Y así, si A’” = B’B” ∩ C’C”, A’” está en el arco capaz de cuerda B’C’ y ángulo CAB.

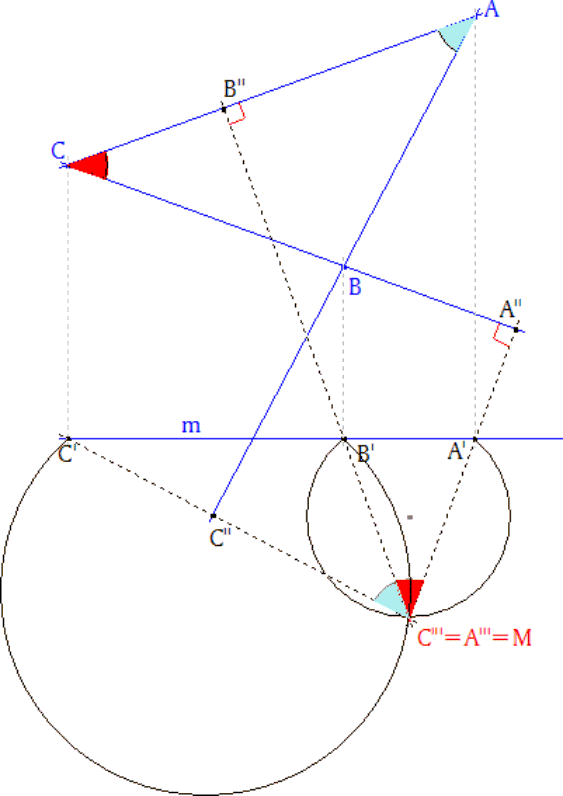
Los dos arcos anteriores se cortan en dos puntos, uno de ellos es B’ el otro es el punto M buscado ya que cumple con las dos propiedades de C’” y A’”.

SEGUNDA PARTE

PASO PREVIO UNO: CIRCULO CIRCUNSCRITO Y CIRCULO DE NUEVE PUNTOS

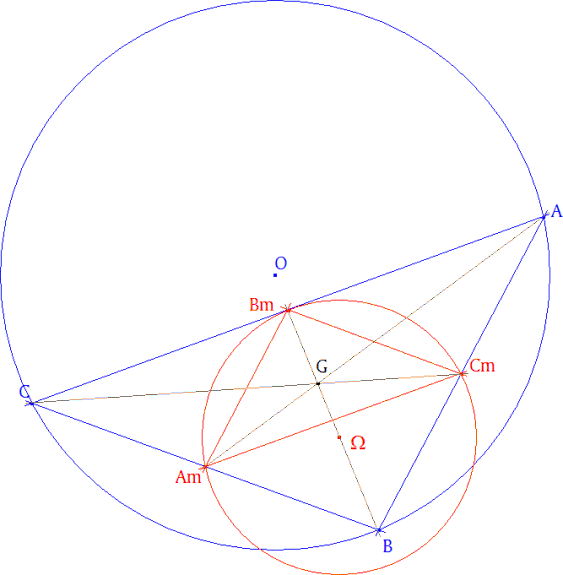
- El círculo circunscrito pasa por A, B, C

- El círculo de nueve puntos pasa por Am, Bm, Cm puntos medios de BC, CA, AB.

Por lo tanto el círculo de nueve puntos es la imagen por una homotecia de razón -1/2.

- Las medianas de ABC se cortan en el baricentro G.

Por lo tanto el centro de dicha homotecia es G.

(Recordemos que entre círculos existen dos homotecias posibles; entonces existirá otra de razón +1/2)

El círculo de nueve puntos es la imagen del círculo circunscrito por una homotecia de razón -1/2 y centro G.

PASO PREVIO DOS: RECTA DE SIMSON

¿Cuál es la condición necesaria y suficiente para que las proyecciones ortogonales de un punto del plano sobre los lados de un triángulo estén en línea recta?

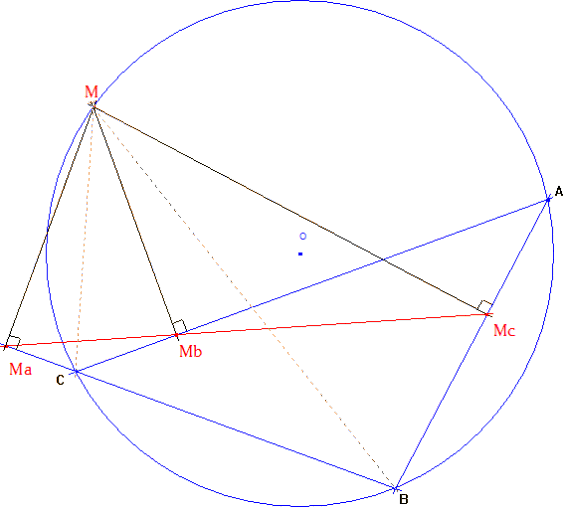
Sea M un punto del plano y Ma, Mb, Mc las proyecciones ortogonales sobre el triángulo ABC.

 - Si Ma, Mb, Mc están alineados, ∠(MaM,MaMb) = ∠(MaM,MaMc). (ángulos orientados salvo módulo(kπ)).

- Pero ∠(MaM,,MaMb) = ∠(CM,CA) ya que M, Ma, Mb y C son cocíclicos.

- Y ∠(MaM,MaMc) = ∠(BM,BA) ya que M, Ma, B, y Mc son cocíclicos.

Nos queda ∠(CM,CA) = ∠(BM,BA) es decir A, B, C y M son cocíclicos

Por lo tanto la condición necesaria y suficiente será que A, B, C y M estén sobre un mismo círculo. Y como el círculo por ABC es el círculo circunscrito podemos decir:

La condición necesaria y suficiente, para que las proyecciones ortogonales de un punto M del plano sobre los lados de un triángulo estén en línea recta, es que M esté sobre el círculo circunscrito. La recta recibe el nombre de recta de Simson (aunque fue descubierta por Wallace).

Tenemos ahora lo necesario para establecer la

SOLUCION

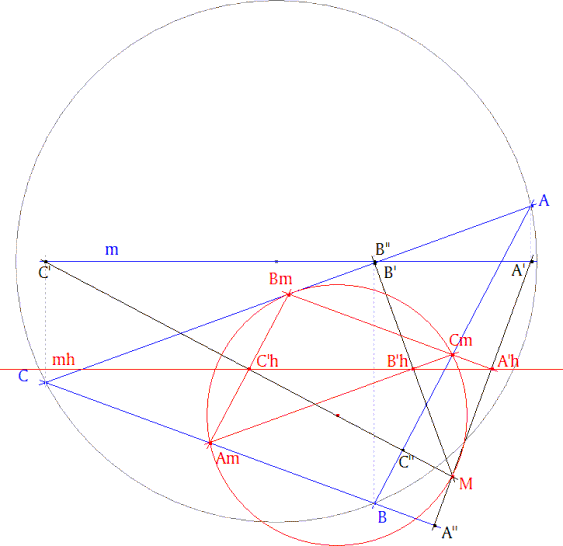
- La proyección de M sobre AmBm es C’h.

- La proyección de M sobre BmCm es A’h.

- La proyección de M sobre CmAm es B’h.

- Por construcción y como m pasa por O, A’h, B’h y C’h son las imágenes de A’, B’ y C’ por una homotecia de centro M y razón +1/2.

- A’, B’, C’ están alineados sobre m,

- La imagen de una recta por una homotecia es una recta

Entonces, A’h, B’h y C’h están sobre una recta y por lo tanto M debe estar sobre un círculo. El círculo debe ser el círculo circunscrito a AmBmCm que a su vez es la imagen por una homotecia de centro G y razón -1/2 del círculo circunscrito de ABC.

Concluimos que M está sobre el círculo de nueve puntos de ABC.