Problema 142
Problema 142
Sea ABC un triángulo rectángulo en A, de hipotenusa a, y catetos b y c.
En la forma que es usual de demostrar el teorema de Pitágoras, hacemos las siguientes construcciones.
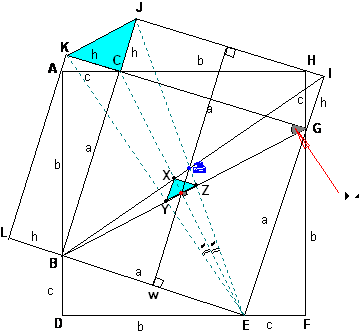
1) Cuadrado ADFH de lado b+c, con la copia de cuatro
triángulos , ABC, en su interior, y el cuadrado BEGC, de lado a.
2) Por los vértices consecutivos A y H del cuadrado,
construimos para cada uno los rectángulos LBCK, CGIJ, tal que KL//BC y
CG//IJ, respectivamente, de área, b c = ah, donde h es la altura de la
hipotenusa.
3) Por último, sean los puntos X, Y, y Z, los puntos de
intersección de las diagonales de los trapecios ICBE, JGEB, GEBK,
respectivamente.
Demostrar que :
a) El triángulo XYZ, es rectángulo e isósceles, y, encontrar
todas las propiedades geométricas del mismo.
b) De toda la figura antes descrita encontrar una nueva
demostración del Teorema de Pitágoras.
c) Si con los vértices F y D del cuadrado se procede por
simetría de la misma forma, en todas las construcciones hechas,
demostrar que el cuadrilátero obtenido es un cuadrado semejante al
cuadrado BEGC. Hallar el centro y la razón de la semejanza.
Romero, J.B. (2004): Comunicación personal
Solución al apartado a) del profesor William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (10 de febrero de 2004)
a) BG es perpendicular a CE (además se cortan en su punto medio) entonces CE es mediatriz de BG
Luego: los triángulos KCE y JCE son iguales (LLL) por lo tanto el triángulo KEJ es isósceles de base KJ. Además los ángulos KEC y CEJ son iguales
Ahora en el triángulo YZE. EC es bisectriz y además perpendicular con GB por lo tanto el triángulo YEZ es isósceles luego se concluye que el cuadrilátero XYEZ es simétrico luego XY = XZ (triángulo XYZ es isósceles)
Ahora solo debemos demostrar que XZ es paralelo a CG
Del gráfico los puntos rojo y azul son los centros del rectángulo y cuadrado respectivamente luego el segmento que los une será perpendicular a los lados del rectángulo y cuadrado y pasará por los punto medios de sus lados
Finalmente en el triángulo isósceles (BTE) TW es altura y por el punto rojo que pertenece a la altura pasan las cevianas BZ y EX (se cumple que XZ es paralelo a BE)
Propiedad antes demostrada
Luego el ángulo Z =45º (del triángulo XYZ)
Finalmente el triángulo xyz es rectángulo e isósceles.