16 de febrero de 2004- 29 de febrero de 2004

Para el aula

Problema 145.

2. Por cualquier punto de la base BC de un triángulo isósceles ABC se levanta una perpendicular que corte a los otros dos lados (o sus prolongaciones) en F y G.

Demostrar que el triángulo AFG es un triángulo isósceles.

Velasco, G. (1983): Tratado de Geometría. Limusa. México. (p. 104)

Nota del editor: Salvando el punto medio de BC, a no ser que se considere el triángulo degenerado AFG donde A=F=G.

Solución de la alumna Maite Peña Alcaraz del Colegio Portaceli de Sevilla (17 de febrero de 2004)

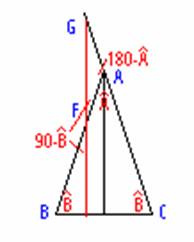
Es evidente por construcción que GFA=(BAC/2) y por tanto vale 90-B y FAG es igual a 180-A, luego puesto que 2B+A=180º, 180º=90-B-180+A+FGA; FGA=270-A+B, y al cambiar A=180-2B, obtenemos que FGA=GFA=90-B por lo tanto AFG es isósceles ya que tiene dos lados iguales.