Problema 145.
Por cualquier punto de la base BC de un triángulo isósceles ABC se levanta una perpendicular que corte a los otros dos lados (o sus prolongaciones) en F y G.
Demostrar que el triángulo AFG es un triángulo isósceles.
Velasco, G. (1983): Tratado de Geometría. Limusa. México. (p. 104)
Nota del editor: Salvando el punto medio de BC, a no ser que se considere el triángulo degenerado AFG donde A=F=G.
Solución de Ricard Peiró i Estruch, profesor de Matemáticas del IES 1 de Xest (València) (15/ 2 / 2004):
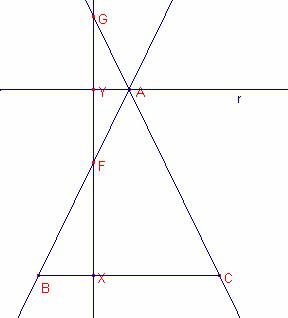
Los ángulos ![]() por ser
opuestos por un vértice.
por ser
opuestos por un vértice.
Consideramos la recta r paralela al lado BC
Los triángulos ![]() son semejantes,
por tanto
son semejantes,
por tanto ![]() .
.
Entonces,
![]() ,
por tanto el triángulo AFG es isósceles.
,
por tanto el triángulo AFG es isósceles.