| Problema 146.- 3. Sea ABC un triángulo cualquiera. Sean los puntos : L sobre AB tal que 2 AL = AB. M sobre BC tal que 3 BM = BC. N sobre AC tal que 4 AN = AC. Si P es la intersección de AM con BN, demostrar que LP es paralela a BC Velasco, G. (1983): Tratado de Geometría. Limusa. México. (p. 105) Nota del editor: Redacción literal, levemente "alterada", sin cambiar el contenido geométrico. |
Solución de la alumna Maite Peña Alcaraz del Colegio Portaceli de Sevilla (17 de febrero de 2004)
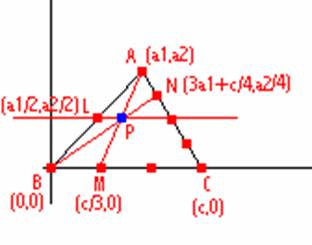
Si hacemos la intersección de AM y BN obtenemos el punto P del cual tan sólo nos interesa la coordenada y, ya que tendrá que ser igual a a2/2.
La recta AM es a2(x-c/3)-(a1-c/3)y=0 y la recta BN es igual a a2x-(3a1+c)y=0, y restando a AM BN, se obtiene lo pedido, luego es evidente que LP es paralelo a BC.