PROBLEMA 146

3. Sea ABC un triángulo cualquiera. Sean los puntos :

L sobre AB tal que 2 AL = AB. M sobre BC tal que 3 BM = BC.

N sobre AC tal que 4 AN = AC.

Si P es la intersección de AM con BN, demostrar que LP es paralela a BC

Velasco, G. (1983): Tratado de Geometría. Limusa. México. (p. 105)

Nota del editor: Redacción literal, levemente "alterada", sin cambiar el contenido geométrico.

Solución del profesor Nicolás Rosillo. Dpto. Matemáticas, IES Máximo Laguna (Santa Cruz de Mudela, Ciudad Real) (16 de febrero de 2004)

 

La configuración inicial puede reducirse a la siguiente:

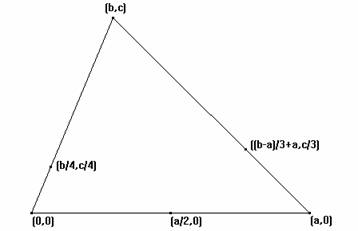
Con A=(0,0), B=(a,0), C=(b,c), L=(a/2,0), M=((b-a)/3+a,c/3) y N=(b/4,c/4)

La recta BN tiene como ecuación

La recta AM tiene de ecuación

El punto P de intersección tiene coordenadas

Y la recta LP es entonces

Como la recta BC es

Se cumple el enunciado