Problema 146.-

Sea ABC un triángulo cualquiera. Sean los puntos :

L sobre AB tal que 2 AL = AB. M sobre BC tal que 3 BM = BC.

N sobre AC tal que 4 AN = AC.

Si P es la intersección de AM con BN, demostrar que LP es paralela a BC

Velasco, G. (1983): Tratado de Geometría. Limusa. México. (p. 105)

Solución de Ricard Peiró i Estruch, profesor de Matemáticas del IES 1 de Xest (València) (17/ 2 / 2004)

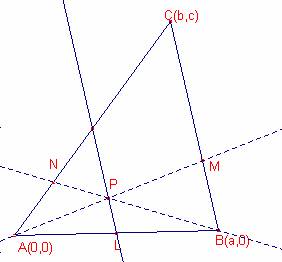
Consideramos el triángulo en coordenadas cartesianas:

A(0, 0), B(a, 0), C(b, c)

Las coordenadas de los puntos L, M, N son:

, 

Sea la recta r que pasa por los puntos A, M su ecuación es:

Sea la recta s que pasa por los puntos B, N su ecuación es:

Determinemos el punt P intersección de las rectas r, s.

Determinemos el vector

Determinemos el vector

Los vectores  son proporcionales,

Por tanto, el segmento LP és paralelo al segmento BC.