Problema 146.- Sea ABC un triángulo cualquiera. Sean los puntos: L sobre AB tal que 2 AL = AB.
M sobre BC tal que 3 BM = BC. N sobre AC tal que 4 AN = AC.
Si P es la intersección de AM con BN, demostrar que LP es paralela a BC.
Velasco, G. (1983): Tratado de Geometría. Limusa. México. (p. 105)
Nota del editor: Redacción literal, levemente "alterada", sin cambiar el contenido geométrico.

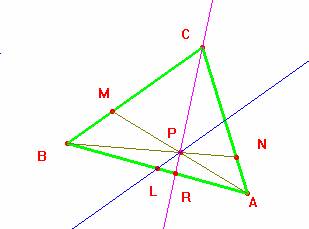
Solución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (17 de febrero de 2004).-
En las condiciones
del problema si trazamos la ceviana CP que
corta al lado opuesto en el punto R, aplicando el teorema de Ceva
obtenemos: ![]() , despejando
, despejando
![]() =2·1/3=2/3.
=2·1/3=2/3.
Si la recta LP no fuera paralela al lado BC, cortaría a éste en el punto Q. Tendríamos en el lado a cuatro puntos alineados: B, M, C y Q.
Si los proyectamos sobre el lado c tomando P
como polo de proyección obtenemos los puntos B, A, R y L. En
este proceso no se altera el valor de la razón doble. Así pues, (B M C
Q) = (B A R L) = ![]() = 3/2.
Por otra parte (B M C Q) =
= 3/2.
Por otra parte (B M C Q) = ![]() :
: ![]() = 3/2 :
= 3/2 :
![]() .
De donde se deduce que
.
De donde se deduce que ![]() = 1, y esto
sólo puede suceder si Q es el punto impropio de la recta BC,
con lo que quedaría probado el paralelismo de esta recta con LP.
= 1, y esto
sólo puede suceder si Q es el punto impropio de la recta BC,
con lo que quedaría probado el paralelismo de esta recta con LP.