Problema 147.-

Sean un triángulo equilátero ABC de lado a, una circunferencia de centro el incentro de ABC y de radio r. Sea P un punto cualquiera de la circunferencia.

Demostrar que:

PA² +PB²+ PC² = a² + 3×r²

Barroso R (2004): Comunicación personal.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

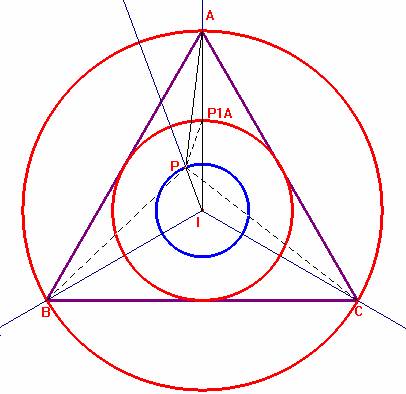
Dado el triángulo equilátero de lado a, construimos sus circunferencias inscrita y circunscrita. Señalamos el punto P_1A como el punto medio del segmento AI, (I, incentro de ABC); por tanto, el punto P₁ pertenecerá a la circunferencia inscrita al triángulo ABC. Asimismo notaremos por x, y, z las longitudes PA, PB y PZ, respectivamente.

Considerando el triángulo IPA, tenemos que:

, es decir:

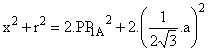
Actuando de un modo semejante con los triángulo IPB e IPC obtendríamos las relaciones:

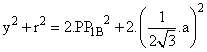
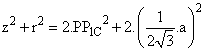
Sumándolas, llegamos a la siguiente expresión:

 (I)

Reiterando el mismo procedimiento ahora para los triángulos IPP_1A, IPP_1B y  IPP_1C, llegaríamos a la expresión:

(II)

Relacionando las expresiones (I) y (II), llegamos a:

 

Observamos que, en el paso al límite, (n>>¥) los puntos P_nA, P_nB y P_nC, llegan a coincidir con el punto I, y así, las longitudes PP_nA, PP_nA, y PP_nA son iguales al radio PI = r.

Por tanto, en el paso al límite, podemos reemplazar el primer paréntesis por esta otra:
 

La última expresión, en el paso al límite, conduce por fin, al resultado deseado: