Problema 149
Teorema de E. Catalan (1814-1894) o circunferencia de Taylor.

a) Si los pies de las alturas de un triángulo se proyectan sobre los otros lados (o rectas que contienen los lados) se obtienen 6 puntos que forman un exágono inscrito en una circunferencia.

b) Tres lados del hexágono son paralelos a los lados del triángulo
                                                                                                                                            

a) Propuesta del profesor Ricard Peiró del IES número 1 de Cheste.
Coolidge, J. L.(1971) A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, pp. 71-73.
b) Añadido por el editor:
Lidski, V. y otros (1978): Problemas de Matemáticas elementales. (p. 58)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

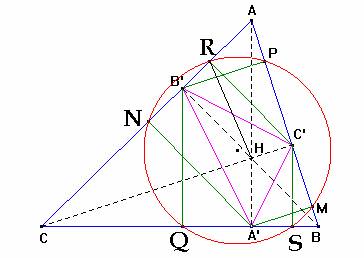a) Consideramos las semejanzas existentes entre los siguientes triángulos notables:

DCNA’~DCQB’;

DCRC’~DCB’H;

DCSC’~DCA’H;

CN/CQ = CA’/CB’ (I)

CR/CB’= CC’/CH (II)

CS/CA’= CC’/CH (III)

Por tanto, de (II) y (III)
[CR/CB’] : [ CS/CA’]= 1; 

Es decir:

CS / CR =  CA’/CB’

Como teníamos (I):      CN / CQ = CA’/ CB’

Entonces: CS / CR =  CN / CQ,  es decir:
CN∙CR = CQ∙CS, lo que significa que los puntos N, R, Q y S son concíclicos. Llamaremos a esta circunferencia que los contiene, C_c.
Si ahora actuamos de igual modo con los puntos Q, S, M y P, determinaríamos la circunferencia C_b y haciendo lo mismo con los puntos M, P, R y N obtendríamos la circunferencia C_a. Veamos que las tres circunferencias son iguales.

Para ello vemos que cada pareja de circunferencias tiene al menos dos puntos en común;  por ejemplo para C_c y C_b serían los puntos Q y S, por lo que el eje radical de dichas circunferencias sería la recta BC = a. Procediendo de la misma forma para cualesquiera otra pareja C_b y C_a , o C_a  y C_c llegamos a la conclusión de que los lados del triángulo inicial ABC serían los ejes radicales de cada uno de los pares de circunferencias considerados y, por tanto no existiría el centro radical de ellas. Como cada par de circunferencias tiene al menos dos puntos en común, resulta que para no llegar al absurdo de la no existencia del centro radical, al menos dos de ellas deberán ser la misma y así de esta forma, la tercera también coincidiría con aquella. Así, las tres circunferencias deben ser una misma circunferencia.
            Por tanto los seis puntos M, N, P, Q, R y S pertenecen, en efecto a una misma circunferencia, LA CIRCUNFERENCIA DE TAYLOR.

b) Veamos ahora que los tres lados del exágono que no pertenecen a los lados del triángulo son paralelos a los lados del triángulo.

En concreto:      NQ  //  AB ,   RP   //  BC   y    MS  //  AC.

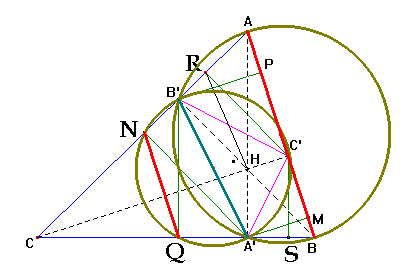Veamos el caso de NQ y AB

Consideramos las circunferencias que pasan por los puntos N, Q, A’ y B’  y la que pasa por los puntos A, B, A’ y B’. Observamos para ello que los puntos N, Q, A’ y B’ son concíclicos (=circunferencia de diámetro A’B’).
De igual manera los puntos A, B,  A’ y B’ pertenecen a la circunferencia de diámetro AB.

En esta situación, el valor de los siguientes ángulos inscritos en aquellas circunferencias será:
<BAB’ = p-<BA’B’ = <B’A’Q = p-<B’NQ = <QNC

En definitiva,

<BAB’ =  <QNC

AC y AB determinan el mismo ángulo que AC y NQ, luego AB y NQ son rectas paralelas.