Problema 149
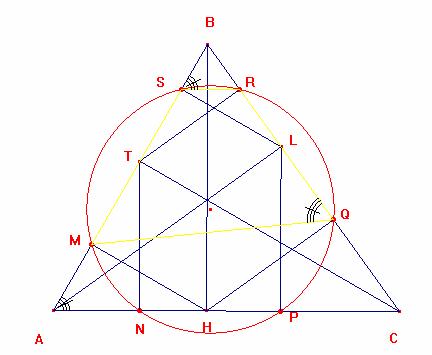
Si los pies de las alturas de un triángulo se proyectan sobre los otros lados (o rectas que contienen los lados) se obtienen 6 puntos que forman un exágono inscrito en una circunferencia.
Solución del profesor William Rodríguez Chamache. profesor de geometría de la "Academia integral class" Trujillo- Perú (2 de marzo de 2004)
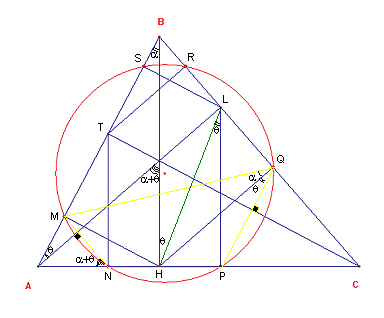
Sea el ángulo MQP = ![]() ; del gráfico
el cuadrilátero MBQH es inscriptible entonces ABH =
; del gráfico
el cuadrilátero MBQH es inscriptible entonces ABH = ![]() ; también
el cuadrilátero LQPH es inscriptible entonces HLP =
; también
el cuadrilátero LQPH es inscriptible entonces HLP = ![]() , y por
alternos internos BHL =
, y por
alternos internos BHL = ![]() ; luego
en el cuadrilátero ABLH inscriptible entonces BAL=
; luego
en el cuadrilátero ABLH inscriptible entonces BAL= ![]() ; se sabe
por propiedad que MN//BC y PQ//AB. Finalmente el cuadrilátero MNPQ es inscriptible
por los ángulos (
; se sabe
por propiedad que MN//BC y PQ//AB. Finalmente el cuadrilátero MNPQ es inscriptible
por los ángulos ( ![]() )
)
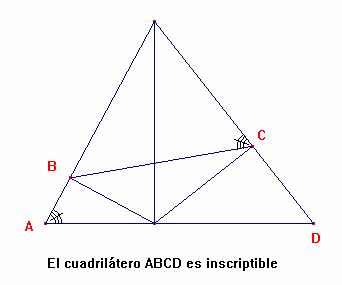
Propiedad:
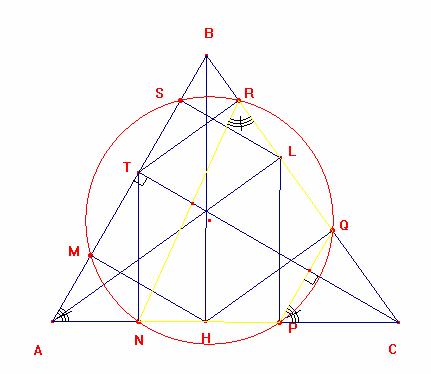
En esta gráfica el cuadrilátero ABRN es inscriptible entonces ángulo A =ángulo NRL y como AB//PQ entonces ángulo A = ángulo QPC; finalmente el cuadrilátero RQPN es inscriptible
Ahora en el gráfico anterior los puntos M, N, P y Q pertenecen a una circunferencia pero en esta gráfica los puntos N, P, Q y R pertenecen también a una circunferencia y como los puntos N, P y Q pertenecen a ambas circunferencias entones loes puntos M, N P, Q y R pertenecen a la misma circunferencia
Observación:
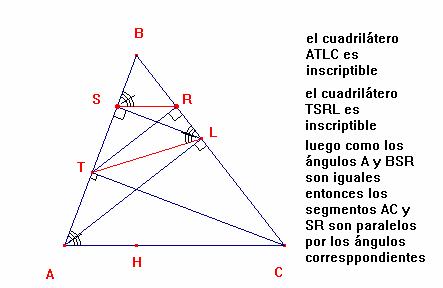
Luego los segmentos SR, PQ y MN son paralelos a los lados del triángulo AC, AB y BC respectivamente
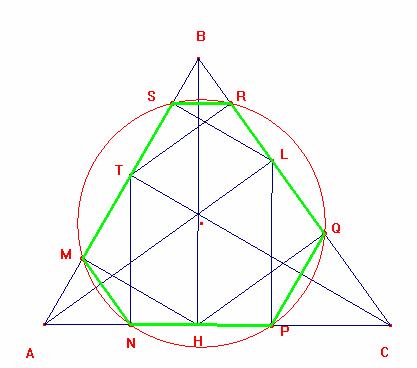
De la misma manera se demuestra que el cuadrilátero MQRS es inscriptible luego los puntos M, Q, R y S también pertenecen al a circunferencia que pasa por los puntos P, Q, R y S finalmente los puntos M, N, P, Q, R y T pertenecen a una misma circunferencia entonces el exágono MNPQRS es inscriptible.
Finalmente se obtendrá la gráfica siguiente:
Prof.: chamache