|
Problema 150.- Sea el triángulo ABC,donde AD y CE son bisectrices
interiores.En la prolongación de ED se toma el punto P, desde el cual
trazamos las perpendiculares PJ,PK y PL sobre AB, BC y AC respectivamente.
Probar que: Salazar, J.L. (2004):
Comunicación personal. |
Solución de Maite Peña Alcaraz (15 de setiembre de
2004):
Tomemos el triángulo A´B´C´
simétrico del que tenemos respecto de la bisectriz exterior de B.
Colocando el eje de coordenadas
en el vértice B que coincide con B` de modo que la bisectriz del ángulo B
coincida con el eje X, obtenemos que si los lados de ABC miden a, b, c, las
coordenadas de los vértices A, B, C y de los puntos D y E son:
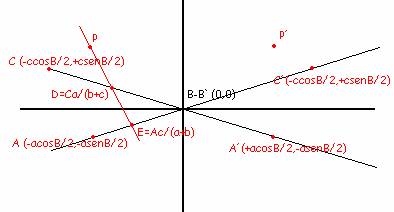
(Los puntos D y E se calculan
sabiendo que por el teorema de la bisectriz EB=ac/(a+b) y DB=ac/(b+c) )
El punto P se puede poner como el
punto E más k veces el director DE, luego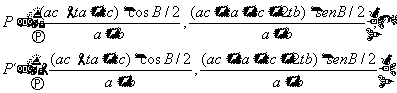 
Siendo t un número cualquiera
positivo. Por ser simétricos es fácil comprobar que la distancia de P a la recta
AC´ (PJ) más la distancia de P` a la
recta AC` es igual a PJ+PL.
La recta AC´ es igual a 
; luego
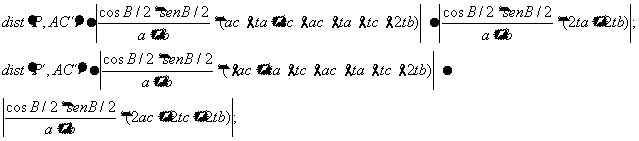Falta calcular la distancia PK, que sabiendo que la recta AC
es: 
entonces la distancia de P a AC será:
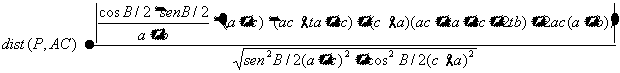y elevando las distancias al
cuadrado y operando se obtiene la igualdad.