Problema 150:

Sea el triángulo ABC, donde AD y CE son bisectrices interiores. En la prolongación de

DE se toma el punto P, desde el cual trazamos las perpendiculares PJ, PK y PL sobre

AB, BC y AC respectivamente. Probar que: PK = PJ + PL.

Demostración: Ver Fig. 1

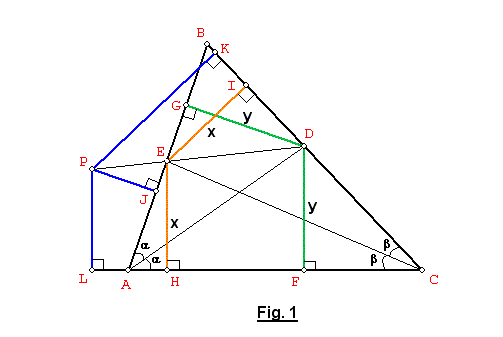
Después de trazar la perpendiculares DG, DF, EI, EH sobre los lados AB, AC, BC, AC respectivamente, asumimos que: EI = EH = x también DG = DF = y. Además se han formado los pares de triángulos rectángulos semejantes:

EGD, EJP donde: … (1)

EID, PKD donde: … (2)

También a partir de los trapecios rectángulos EHFD y PLHE: ... (3)

A partir de (1): ; por lo tanto:

Entonces, por propiedad de proporciones:

Finalmente:

PK = PJ +PL QED.

Juan Carlos Salazar

caisersal@yahoo.com