Problema 151.- En un triángulo acutángulo ABC, AA₁,BB₁ y CC₁ son alturas, A₁B₁ corta a  CC₁ en E, AA₁ corta a B₁C₁ en D. La recta DE corta a AB y BC en P y Q. Probar que Ángulo(PB₁C₁) = Ángulo(QB₁A₁) y además que AQ, CP y BB₁ son concurrentes.

Solución del profesor Saturnino Campo Ruiz, del IES Fray Luis de León de Salamanca (5 de marzo de 2004)  .-

 

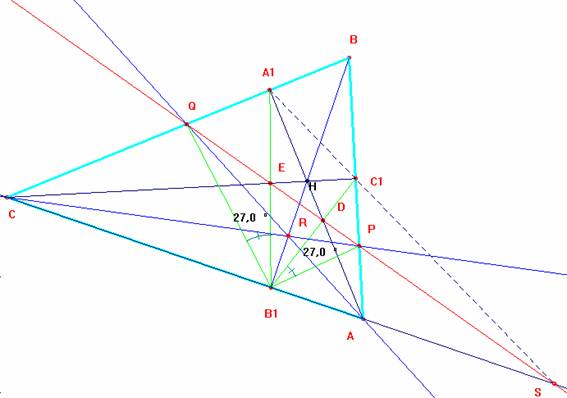
1º.- Comenzaremos con la concurrencia de las rectas AQ, CP y  BB₁. Tomando como sistema de referencia proyectivo el triángulo ABC  y punto unidad el ortocentro H, los diferentes puntos y rectas vienen representados como sigue:

Puntos: A= l(1,0,0); B= l (0,1,0); C = l (0,0,1); A₁ = l (0,1,1); B₁ = l (1,0,1); C₁ = l (1,1,0);

Rectas: A₁B₁:  z = x + y ;A₁C₁:  y = x + z ; B₁C₁:  x = y + z; AA₁:  y = z;  CC₁: y = x;  BB₁:  x = z.

El punto D, intersección de B₁C₁  con AA₁  es D = l (2,1,1) en cuanto al E, que lo obtenemos como intersección de las rectas A₁B₁ y CC₁ es E= l (1,1,2).

La recta DE tiene ecuación x—3y + z = 0  y corta a los lados AB (z=0) en P= l (3,1,0) ;  BC (x=0) en  Q= l (0,1,3)  y AC (y=0) en  S= l (1,0,-1).

Las rectas determinadas por C yP x=3y , por  A y Q 3y=z  se cortan en R= l (1,3,1) que también pertenece a la recta BB₁ ,  x= z  con lo que se concluye la concurrencia.

Puede comprobarse, aunque no es necesario para lo que pretendemos que las rectas A₁C₁, PQ y AC concurren en S, que, como vamos a ver a continuación es el cuarto armónico de los puntos alineados B₁, A y S. Como puede observarse, en ningún momento se ha utilizado el hecho de ser H el ortocentro del triángulo, y es que, la propiedad demostrada es cierta para tres cevianas cualesquiera sin ninguna condición previa sobre ellas.

2º.-  Las alturas del triángulo ABC son bisectrices del  triángulo órtico A₁ B₁C_1.Para demostrar que los ángulos <PB₁C₁  y <QB₁A₁ son iguales bastará con probar que la altura BB₁ es la bisectriz del ángulo QB₁P. Aunque ya se demostró en el problema nº 71 (teorema de Blanchet), lo repetimos ahora.

Según el teorema de Ceva para las rectas concurrentes en R se tiene: y, según el teorema de Menelao para el triángulo ABC cortado por la transversal PQ:    . Si las multiplicamos entre sí queda  que nos indica que los puntos alineados B₁ ,S, A y C forman una cuaterna armónica, y esto, según el teorema de la bisectriz, implica que BB₁  es la bisectriz interior del ángulo <QB₁P, como se deseaba demostrar.