Problema 151.- En un triángulo acutángulo ABC, AA₁,BB₁ y CC₁ son alturas, A₁B₁ corta a  CC₁ en E, AA₁ corta a B₁C₁ en D. La recta DE corta a AB y BC en P y Q. Probar que Ángulo(PB₁C₁) = Ángulo(QB₁A₁) y además que AQ, CP y BB₁ son concurrentes.

Solución del profesor Saturnino Campo Ruiz, del IES Fray Luis de León de Salamanca (4 de marzo de 2004).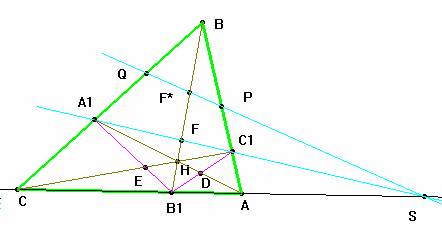

1º.- Si se tienen tres cevianas cualesquiera AA₁,BB₁ y CC₁, que concurren en un punto H, la recta A₁C₁  corta al lado AC en el punto S, tal que la cuaterna (C A B₁ S) es armónica.

En efecto, según el teorema de Ceva para las rectas concurrentes en H se tiene:   y, según el teorema de Menelao para el triángulo ABC cortado por la transversal A₁C₁:    . Multiplicándolas entre sí sale .

Al conservarse la razón doble por proyección tendremos que también son armónicas las cuaternas (A₁ C₁ F S) y (Q P F* S) , ésta última obtenida por las secciones en ABC de una recta arbitraria que pasa por S, y recíprocamente si la cuaterna (A₁ C₁ F S) es armónica, entonces las rectas  MM₁ son cevianas, operando como antes.  (Si (A₁ C₁ F S) es armónica, y los puntos Q, P y F* se proyectan desde B sobre los puntos A₁, C₁  y F, el cuarto armónico de ellos, por ser único, ha de ser necesariamente el punto S común a ambas series).

Si ahora nos fijamos en la recta SQ, por ser armónica (Q P F* S), tendremos que también son cevianas concurrentes las rectas CP, AQ y B₁B.

Aplicando estos razonamientos generales a nuestro problema con las tres alturas, tendremos ya la concurrencia de las rectas AQ, CP y  BB₁.

 

 

 

 

 

 

 

 

 

 

 

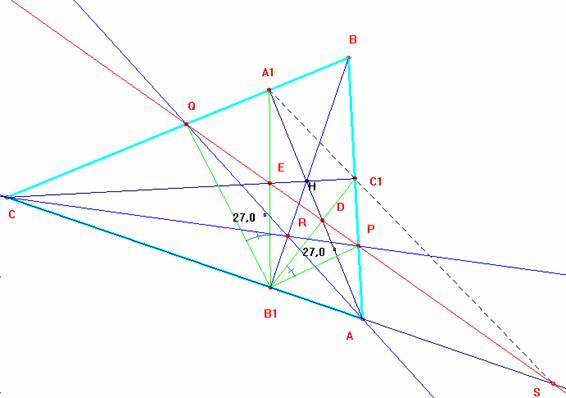
2º.-  Las alturas del triángulo ABC son bisectrices del  triángulo órtico A₁ B₁C_1.Para demostrar que los ángulos <PB₁C₁  y <QB₁A₁ son iguales bastará con probar que la altura BB₁ es la bisectriz del ángulo QB₁P. Ya se demostró en el problema nº 71 (teorema de Blanchet), y aquí mismo se ha demostrado ya, pues, como hemos visto, los puntos alineados C, A, B₁  y S, forman una cuaterna armónica, y esto, según el teorema de la bisectriz, implica que BB₁  es la bisectriz interior del ángulo <QB₁P, como se deseaba demostrar.