Problema 153
El área de un triángulo rectángulo es igual al producto de los segmentos
determinados en la hipotenusa por la circunferencia inscrita.
Propuesto por el profesor Ricard Peiró
del IES número 1 de Cheste
LEVI S. SHIVELY, PH.D. (1972) Introducción a la
Geometría Moderna. Compañia editorial continental.
Mèxico. pàg.
171.
Bruño(1963), Geometría Curso Superior , pág 250, prob 523.
Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante, de Córdoba.
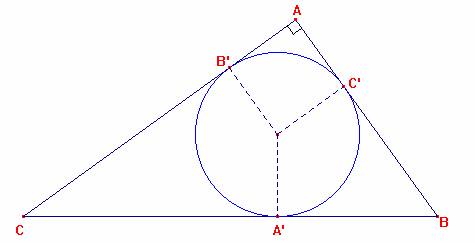
Dada la figura anterior, sabemos que los segmentos determinados en la hipotenusa por el punto de contacto A’ de la circunferencia inscrita miden CA’=p-c y BA’=p-b, donde 2p= a+b+c
Por tanto, el producto CA’·A’B= (p-c)· (p-b) = 1/4 ·(a+b-c)·(a-b+c);
Es decir:
CA’·A’B= 1/4 ·(a2 -(b-c)2 )= 1/4·( a2 - b2 - c2 + 2·b·c)= 1/2· b·c= S(ABC)
ya que: a2 = b2 + c2