PROBLEMA 153

Solución del profesor Nicolás Rosillo.

Dpto. Matemáticas, IES Máximo Laguna.

Santa Cruz de Mudela, Ciudad Real

nrosillo@olmo.pntic.mec.es

El área de un triángulo rectángulo es igual al producto de los segmentos determinados en la hipotenusa por la circunferencia inscrita.

Para esta demostración se hace uso del enunciado del problema 57:

En un triángulo rectángulo, el radio de la circunferencia inscrita mide , con a y b catetos y c hipotenusa.

Sin pérdida de generalidad, se puede suponer una configuración como la siguiente:

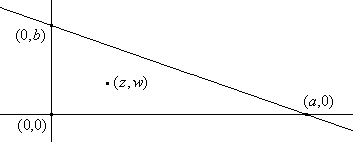
Las coordenadas del incentro (z,w) son por tanto

Se halla la recta que pasa por (a,0) y (0,b), y se obtiene la perpendicular a ella que pasa por el incentro (imágenes capturadas del programa DERIVE versión 5.02):

A continuación se obtiene el punto de intersección (c,d) de ambas rectas.

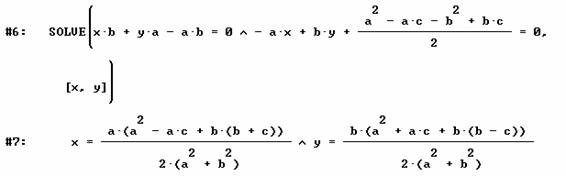
Se halla el cuadrado del modulo del segmento (c,d)(0,b). No se usa el módulo a fin de evitar la aparición de valores absolutos en el resto del proceso de cálculo.

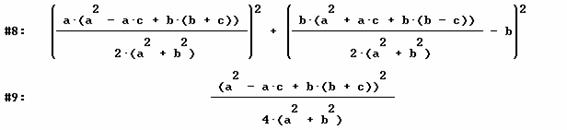
Y el cuadrado del modulo del segmento (c,d)(a,0)

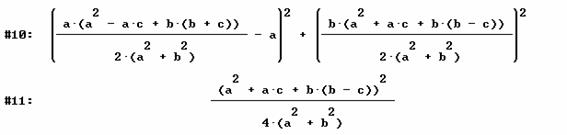
Al hacer el producto de ambos módulos

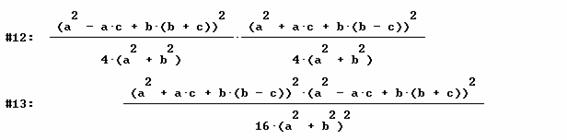
Y sustituir c por

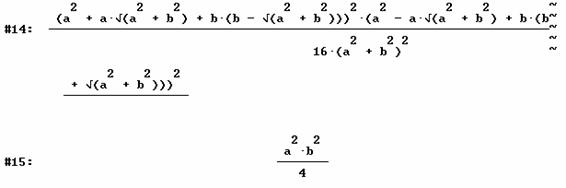
Se obtiene el cuadrado del área del triángulo, por lo que el enunciado del problema queda demostrado.