Problema 153

El área de un triángulo rectángulo és igual al producto de los segmentos determinados en la hipotenusa por la circunferencia inscrita.

LEVI S. SHIVELY, PH.D. (1972) Introducción a la Geometría Moderna. Compañia editorial continental. Mèxico. pàg. 171

Bruño(1963), Geometría Curso Superior , pág 250, prob 523.

Dos soluciones de Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz). (24 de marzo de 2004)

En la figura mostrada, tenemos:

                        

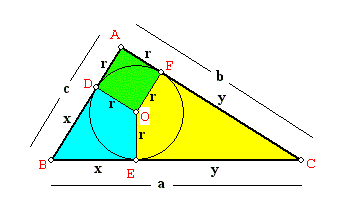
<A = 90º, D, E, F son puntos de tangencia con el incírculo O, de radio r.

Entonces:

AreaABC = (1/2) AC.AB = (1/2) b.c = (1/2) (r+x) (r+y) = (1/2) [r² + r(x+y) + x.y]

2Area ABC = r² +r(x+y) + x.y……... (1)

También:

AreaABC = Area OFAD + Area ODBE + Area OECF

AreaABC =  r² + r.x + r.y = r² + r(x+y)…… (2)

Reemplazando (2) en (1): Area ABC = x.y      LQQD.

Solución 2: Ver la figura anterior

Por Herón, con p = semiperímetro

Area ABC² = p (p-a) (p-b) (p-c)…… (1)

Para este caso particular: (p-a) = r, (p-b) = x, (p-c) = y,  también: Area ABC = p.r

Reemplazando en (1):

Area ABC² = p.r.x.y = Area ABC.x.y

Area ABC = x.y.       LQQD.