Problema 156.-
Sean ABCD un cuadrilátero cualquiera, P y Q los puntos medios de los lados opuestos DC y AB respectivamente. Sea X la intersección de los segmentos DQ y AP e Y la intersección de QC y PB. ¿Qué relación hay entre las áreas del cuadrilátero PXQY y la de los triángulos ADX y BCY?
Propuesto por los profesores Jesús Murillo Ramón y Jose Francisco Martín Olarte
Dto de Matemáticas y Computación de la Universidad de La Rioja

Murillo, J. y Martín, J.F. (2004): Propuesta personal.,

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante, de Córdoba.

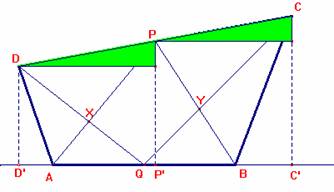Considerando la figura adjunta, observamos que los segmentos DD’, PP’ y CC’, perpendiculares a la recta AB por los puntos D, P y C, respectivamente verifican la siguiente relación

 como se puede deducir de forma inmediata a partir de los triángulos rectángulos iguales coloreados en verde.

Por tanto, si representamos por [APB] el valor del área del triángulo APB, tenemos que:

[APB] = 1/2∙ AB∙PP’= 1/2∙ (AQ + QB)∙1/2∙ (DD’ + CC’), desarrollando:

[APB] = 1/2∙(1/2∙AQ∙DD’+1/2∙AQ∙CC’+ 1/2∙QB∙DD’+1/2∙QB∙CC’);
y teniendo en cuenta que AQ = QB, llegamos a:

[APB] = 1/2∙( [AQD]+[QBC]+ [AQD]+[QBC] )= [AQD]+[QBC];

En definitiva:
[APB] = [AQD] + [QBC]       (i)

De igual modo, probaríamos que:

[DQC] = [DPA] + [PCB]       (ii)

Sumando ambas expresiones obtenidas (i) y (ii), llegamos a la siguiente relación:

[APB] + [DQC] =  [AQD] + [QBC] + [DPA] + [PCB]

Por un lado:    

[APB] + [DQC] =  2∙[PXQY] + [AXQ] + [QYB] + [DXP] + [PYC]
Por otro lado:  

[AQD] + [QBC] + [DPA] + [PCB] = [ADX] + [AXQ] + [QYB]+ [BCY]+ [DXP]+ [AXD]+ [PYC]+ [BCY]

Simplificando los términos comunes en ambas expresiones llegamos por fin a:

2∙[PXQY] = 2∙ [ADX] + 2∙[BCY]

En definitiva,
[PXQY] = [ADX] + [BCY]

que muestra la relación existente entre las áreas del cuadrilátero PXQY y la de los triángulos ADX y BCY, c.q.d.