PROBLEMA 156

Solución del profesor Nicolás Rosillo.

Dpto. Matemáticas, IES Máximo Laguna.

Santa Cruz de Mudela, Ciudad Real

nrosillo@olmo.pntic.mec.es

Sean ABCD un cuadrilátero cualquiera, P y Q los puntos medios de los lados opuestos DC y AB respectivamente. Sea X la intersección de los segmentos DQ y AP e Y la intersección de QC y PB. ¿Qué relación hay entre las áreas del cuadrilátero PXQY y la de los triángulos ADX y BCY?

Sin pérdida de generalidad, se puede suponer una configuración como la siguiente:

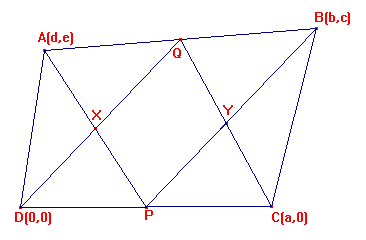
Se usan dos funciones definidas con anterioridad a fin de agilizar cálculos (imágenes capturadas del programa DERIVE versión 5.02):

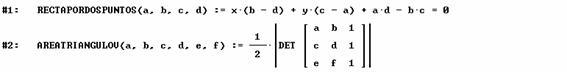
Se obtiene las rectas que pasan por DQ y PA y el punto de intersección X de ambas.

Si se consideran los parámetros a,b,c,d y e del inicio de problema positivos no nulos, el numerador del punto X es positivo, y su denominador también.

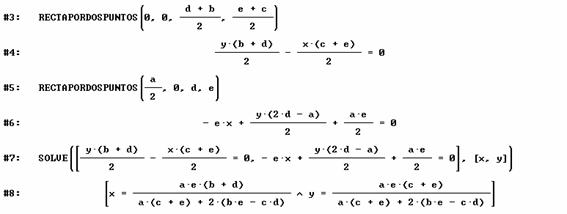
Se obtiene las rectas que pasan por PB y CQ y el punto de intersección Y de ambas.

Si se consideran los parámetros a,b,c,d y e del inicio de problema positivos no nulos, el numerador del punto Y es positivo, y su denominador también.

Cálculo del área del triángulo ADX

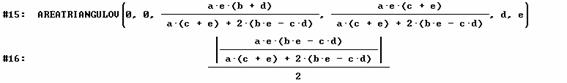
Cálculo del área del triángulo PXQ

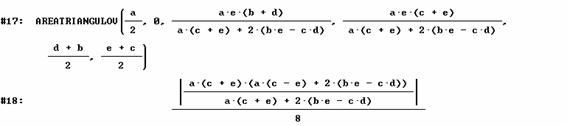
Cálculo del área del triángulo PYQ

Cálculo del área del triángulo BCY

Por el motivo argumentado en la obtención de signos de los numeradores y denominadores de X e Y, se pueden suprimir los valores absolutos de las expresiones de las áreas. Si se sumas áreas de ADX y BCY y se restan las de PXQ y PYQ se obtiene cero, por lo que el área del cuadrilátero PXQY es igual a la suma de las de los triángulos ADX y BCY.