Propuesto por los profesores Jesús Murillo Ramón y Jose Francisco Martín Olarte

Dto. de Matemáticas y Computación de la Universidad de La Rioja

Problema 156.

Sean ABCD un cuadrilátero cualquiera, P y Q los puntos medios de los lados opuestos DC y AB respectivamente. Sea X la intersección de los segmentos DQ y AP e Y la intersección de QC y PB.

¿Qué relación hay entre las áreas del cuadrilátero PXQY y la de los triángulos ADX y BCY?

Murillo, J. y Martín, J.F. (2004): Propuesta personal.

Solución de José María Pedret. Ingeniero Naval. Esplugas.

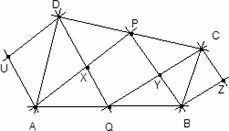a          completamos el triángulo ADX hasta el paralelogramo AUDX.

b          completamos el triángulo BCY hasta el paralelogramo BZCY.

c          por construcción de P, Q, X, Y, el cuadrilátero QXPY es la media aritmética de los paralelogramos anteriores.

d          los paralelogramos anteriores tienen el área el doble de los triángulos.

e          Entonces el área del cuadrilátero es igual a la suma de los dos triángulos.