|
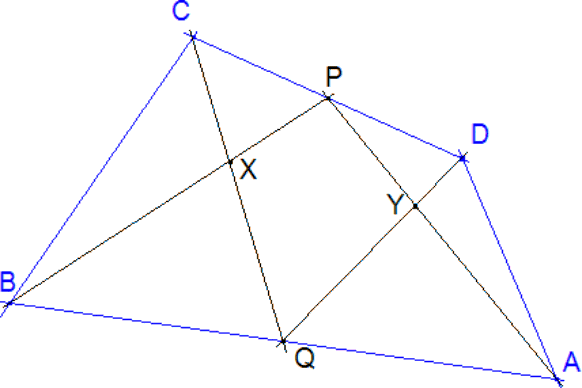
Propuesto por los profesores Jesús Murillo Ramón y Jose Francisco Martín Olarte Dto de Matemáticas y Computación de la Universidad de La Rioja Problema 156.- Sean ABCD un cuadrilátero cualquiera, P y Q los puntos medios de los lados opuestos DC y AB respectivamente. Sea X la intersección de los segmentos DQ y AP e Y la intersección de QC y PB. ¿Qué relación hay entre las áreas del cuadrilátero PXQY y la de los triángulos ADX y BCY? Murillo, J. y Martín, J.F. (2004): Propuesta personal. | ||
|
| ||
|
QUIERO DEDICAR ESTA SOLUCION A RICARDO BARROSO CAMPOS. En atención a Ricardo y a sus trianguloscabri, buscamos la solución usando sólo triángulos y sus propiedades. Y claro, sólo con regla y compás (cabri).Segnda solución de José María Pedret. Ingeniero Naval. Esplugas. | ||
| ||
|
| ||
|
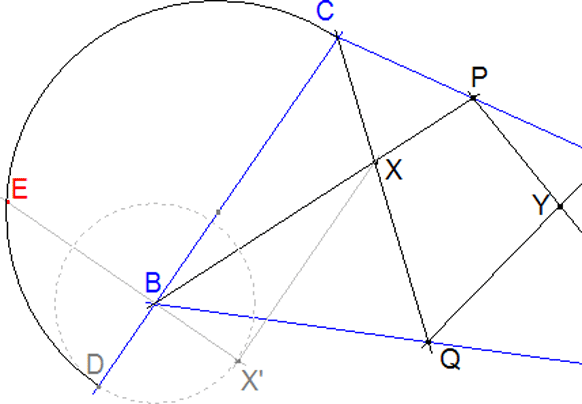
PRIMER PROBLEMA PREVIO ¿ Cuál es el triángulo rectángulo e isósceles que tiene la misma área que un triángulo dado? (Aplicación al triángulo BXC) | ||
| ||
Area CBX = ½CBBX’. Extendemos CB hasta CD con BD = BX’. Trazamos la perpendicular a CD por B. La intersección E de esa perpendicular con el círculo de diámetro CD cumple: CBBD = BEBE = CBBX’. BE es el cateto del triángulo rectángulo isósceles cuya área es igual a la del triángulo dado BXC. | ||
|
| ||
|
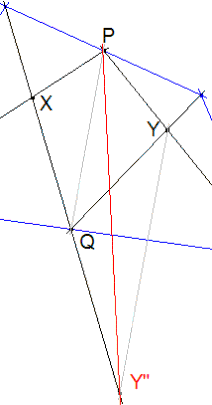
SEGUNDO PROBLEMA PREVIO ¿ Cuál es el triángulo rectángulo e isósceles que tiene la misma área que un cuadrilátero dado? (Aplicación al cuadrilátero PXQY) | ||
|
PRIMER PASO Convertir el cuadrilátero en un triángulo de igual área. Tomámos el triángulo PQY. Por Y paralela YY” a PQ. Manteniendo la base PQ, cualquier punto sobre YY” conserva el área igual al área PQY. En particular, Y” en la intersección con XQ. Por tanto: área PQY= área PQY” y entonces área QXPY = área XPY” | |
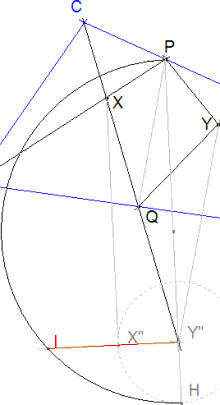
|
SEGUNDO PASO Convertir el triángulo XPY” en un triángulo rectángulo isósceles de igual área. Recordando el primer problema previo: Extendemos PY” hasta PH con Y”H = Y”X”. Perpendicular en Y” a PH. Obtenemos I en la intersección de la perpendicular con el círculo de diámetro PH. PY”Y”H = Y”IY”I. Y”I es el cateto del triángulo buscado. | |
|
| ||
|
TERCER PROBLEMA PREVIO ¿ Cuál es el triángulo rectángulo isósceles que tiene la misma área que dos triángulos rectángulos isósceles dados? | ||
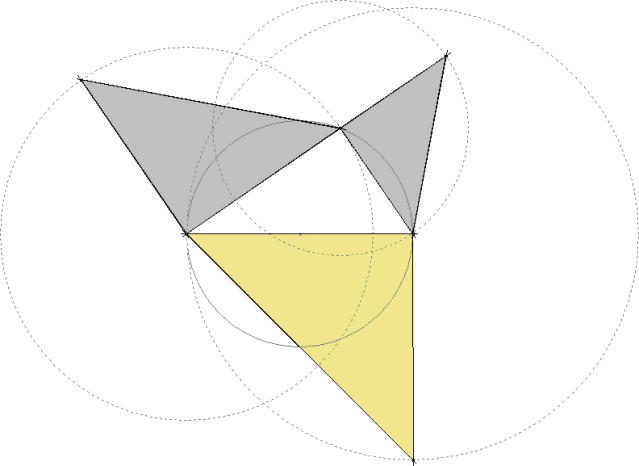
| ||
|
Sin palabras: Sólo basta recordar el teorema de Pitágoras. Los triángulos dados son los triángulos grises. El triángulo solución, el amarillo. | ||
|
| ||
|
| ||
|
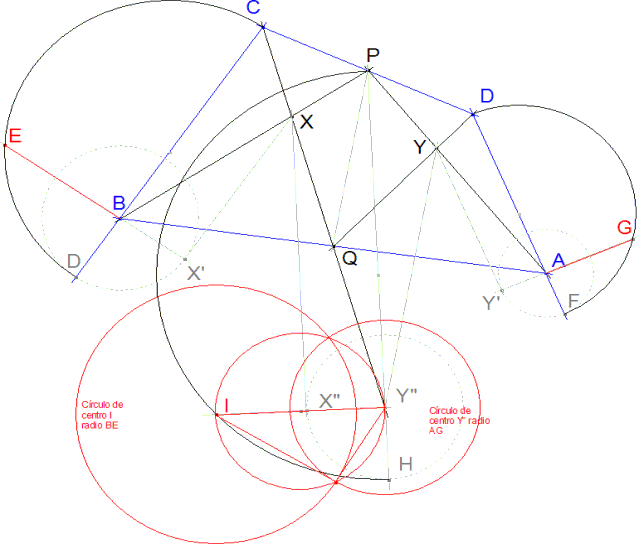
Con todo lo visto, ya podemos responder al problema propuesto | ||
| ||
|
a |
Hallamos el cateto equivalente BE (primer problema previo) del triángulo BXC. | |
|
b |
Hallamos el cateto equivalente AG (primer problema previo) del triángulo AYD. | |
|
c |
Hallamos el cateto equivalente Y”I (segundo problema previo) del caudrilátero PXQY. | |
|
d |
Comprobamos (tercer problema previo) que los tres catetos hallados forman un triángulo rectángulo de catetos BE y AG e hipotenusa Y”I (Intersección te círculos rojos). | |
|
|
| |
|
Hemos demostrado que la suma de las áreas de los triángulos BXC y AYD es igual al área del cuadrilátero PXQY. | ||