Problema 156.-

Sean ABCD un cuadrilátero cualquiera, P y Q los puntos medios de los lados opuestos
DC y AB respectivamente. Sea X la intersección de los segmentos DQ
y AP e Y la intersección de QC y PB. ¿Qué relación hay entre las áreas del
cuadrilátero PXQY y la de los triángulos ADX y BCY?

Solución del profesor William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú

En la figura observamos que la parte sombreada es igual a S1+ S2

Donde Q y P son puntos medios de AB y CD

                                                                                

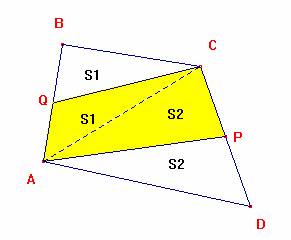
                                 Del gráfico observamos que:

                              S + A + B + m  = R + y +x +n ........ (1)

                                 Tambien  observamos que:

                              R + A +B + n =  y + m + x +s   ........ (2)

                                             Sumando  (1) y (2)

                                                    A + B = x + y

                                                   Finalmente se demuestra que:

                                                              QXPY =   BYC + AXD   

Prof.: chamache