Problema 157
Propuesto por Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).
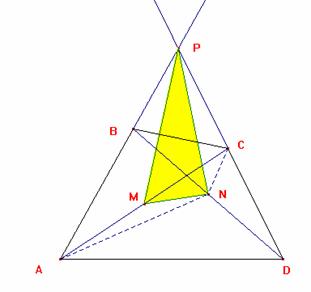
En un cuadrilátero convexo ABCD, las prolongaciones de AB y DC se cortan en P.
Si los puntos medios de AC y BD son M y N respectivamente, demostrar que
el área
del triángulo MNP es 1/4 del área de ABCD.
Posible autor Th. Caronnet
El editor y el proponente del problema agradece a Darij Grinberg
de Karlsruhe (Germany) la referencia de este problema.
Coxeter, H.S.M. y Greitzer, S.L.(1993): Retorno a la Geometría. La tortuga de Aquiles, Traducción de Pedro Gómez y Joaquín Hernández. ( La tortuga de Aquiles). (pag 54)
Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (5 de marzo de 2004)
Recordemos la siguiente propiedad.
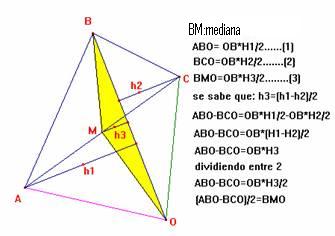
Sea S el área del cuadrilátero ABCD
Luego del gráfico se observa que: S = APD – BPC
Pero: APN = APD/2 y PNC = BPC/2 restando estas dos expresiones obtenemos:
APN – PNC = 
APN – PNC = 
APN – PNC = 
Ahora observen el triángulo ANC (MN es mediana y P un punto exterior)
Entonces se cumple la propiedad mencionada al inicio.
Por lo tanto: 
finalmente
obtenemos: 
