Propuesto por Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).

Problema 158

Sea el triángulo ABC inscrito en un circulo (O) . El Circulo (K1)está dentro de  del triángulo y es tangente a los lados AB, AC en M1, N1 y también es tangente al círculo (O) en P1. Los puntos M2, N2, P2 y M3, N3, P3 son definidos similarmente para los ángulos B y C respectivamente. Probar que M1N1,M2N2 y M3N3 se intersecan entre ellos en sus puntos medios.

Foro de Internet Hyacinthos

 Solución de José María Pedret, Ingeniero Naval. Esplugas. 16 de abril de 2004

TRAZADO DEL ENUNCIADO

Dibujar el enunciado ya es en sí un problema. Determinar M1, N1 y P1 equivale a trazar el círculo tangente a dos rectas y un círculo, una de las diez posibilidades del problema de Apolonio. Hay diversas maneras de hallarlo. Quien esté interesado puede consultar la excelente página de Francisco Javier García Capitán BELLA GEOMETRIA.

PARA HACERLO, NOSOTROS USAREMOS LA INVERSION; PERO TRAZANDO SOLO UN CIRCULO Y ¡SIN INVERTIR!

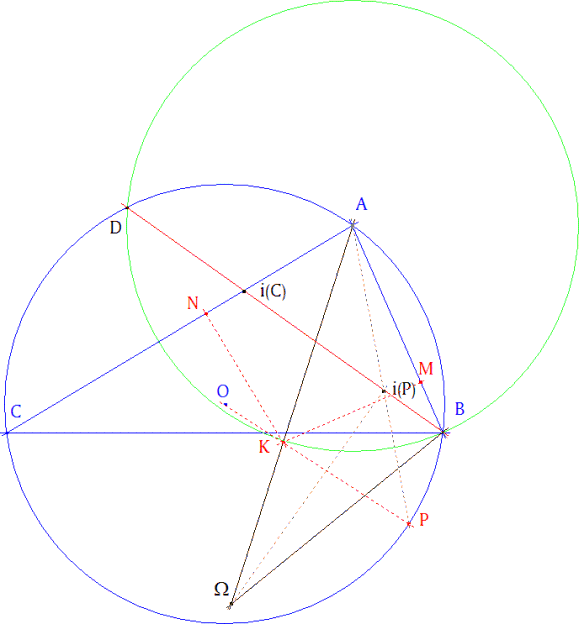
- Lo más fácil es buscar tangencias con rectas (y no con círculos). Invertiremos el círculo circunscrito O usando, para la inversión, otro círculo cuyo centro esté en el círculo O. El transformado del círculo circunscrito es una recta.

- Elegiremos el círculo de centro A y que pasa por B.

¿Por qué elegimos este círculo?

Al estar el centro en A, AB, AC, y la bisectriz de ∠BAC no cambian por la inversión. Todas pasan por A y el punto B es inverso de sí mismo.

- La figura inversa del círculo circunscrito es la recta BD. D es la segunda intersección del círculo de inversión y el círculo circunscrito O.

- La intersección de BD con AC es i(C), inverso de C.

Hemos sustituido dos rectas y un círculo por tres rectas. Buscar el círculo tangente equivale a buscar el círculo inscrito a las tres rectas AB, AC y BD.

De los cuatro círculos posibles, sólo nos interesa el círculo ex-inscrito opuesto a A.

¿Por qué?

Porque una vez deshecha la inversión, éste queda en el interior del triángulo ABi(C). Acorde con la solución buscada.

- Determinamos Ω centro del círculo ex-inscrito que nos interesa, como la intersección de la bisectriz de ∠CAB y la perpendicular a la bisectriz ∠ABC. (Esto de la perpendicular es para ahorrar puntos construidos).

- El punto de tangencia i(P) sobre BD, se halla por la perpendicular desde Ω a BD. A su vez i(P) no es más que el inverso de P, que es el punto de tangencia sobre O que estamos buscando.

- Para hallar P a partir de i(P), trazanos la recta que une A con i(P). P estará en la intersección de esta recta con el círculo inscrito.

- El centro del círculo K, estará en la intersección de la bisectriz de ∠CAB y la recta OP.

- Desde K perpendiculares a AB, AC y obtenemos los puntos M y N respectivamente.

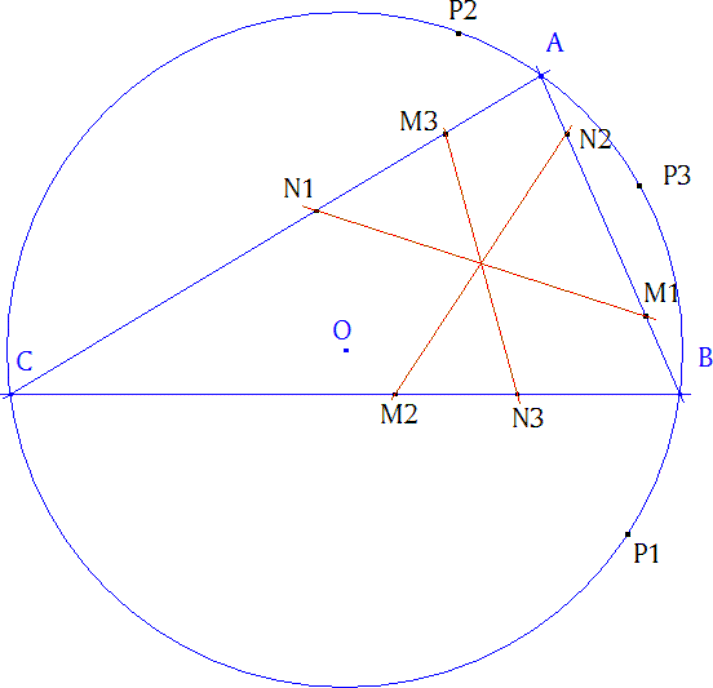
MACRO PARA CABRI

(guardar el archivo en un directorio del disco duro.

abrir el programa Cabri. Archivo, abrir, tipo archivos de macro, y buscar en el directorio el archivo "bajado" C_tg_rrc.mac, que se incorporará como una macro en el menú de Cabri (NOTA del editor))·.

 Objetos iniciales: tres puntos C, A, B (en este orden)

 Objetos finales tres puntos M, N, P

 Texto “Seleccionar tres puntos C, A, B y obtenemos los puntos de tangencia M, N, P de un círculo inscrito en el interior de ∠CAB y el círculo circunscrito a ABC.”

Usamos ahora la macro tres veces. Vemos que el enunciado se cumple. Cabri ya ha hecho su trabajo, ahora nosotros también debemos demostrarlo.

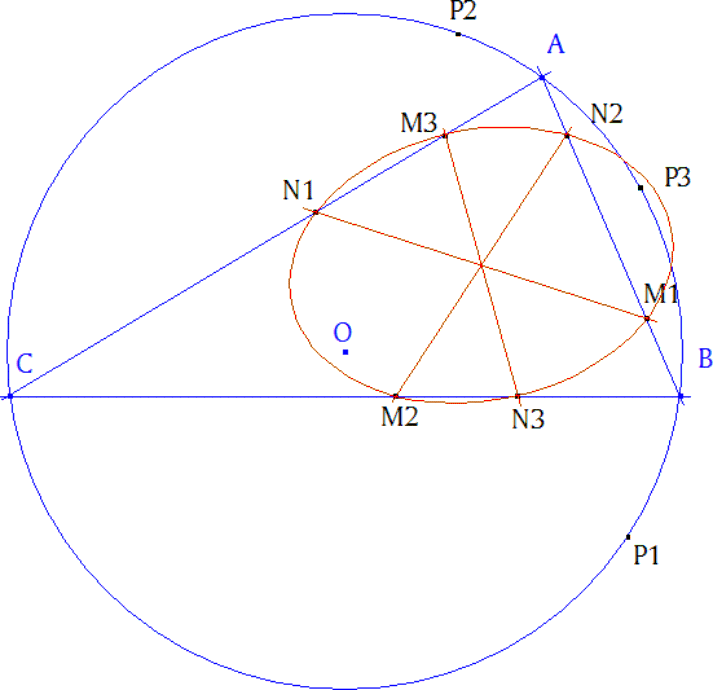
UN POCO MAS DE MAGIA CABRI - ¿Una cónica?

Observando la figura anterior, es claro que los punto M, N... poseen alguna relación. Haciendo uso y abuso de cabri, trazando la cónica por cinco de los seis puntos, parece que los seis están sobre una cónica.

Se puede demostrar que es así y para solucionar el problema, basta demostrar que M1N1, M2N2, M3N3 son diámetros de una cónica.

Pero hay otra solución muy sencilla.

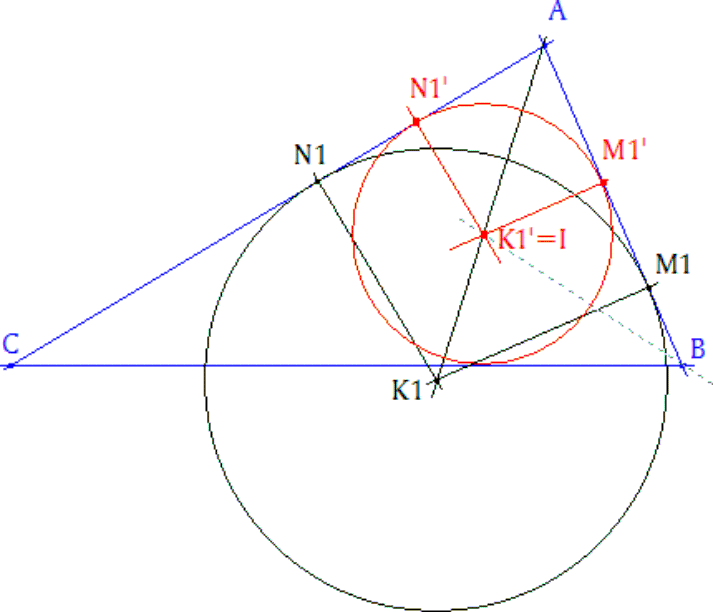
UNA SOLUCION USANDO SOLO LOS ELEMENTOS

Si recordamos el enunciado, K1 es el centro del círculo M1N1P1. M1 y N1 son los puntos de contacto del círculo con los lados AB y AC, M1 y N1 equidistan de la bisectriz de ∠CAB. Su punto medio está sobre dicha bisectriz.

¿Cuál es el círculo homotético de M1N1P1 con centro de homotecia en A y que es tangente al lado CB?

Este círculo será tangente a los tres lados del triángulo; por tanto, es el círculo inscrito al triángulo ABC.

 I es el centro del círculo inscrito al triángulo. I es la imagen de K1 por una homotecia de centro en A.

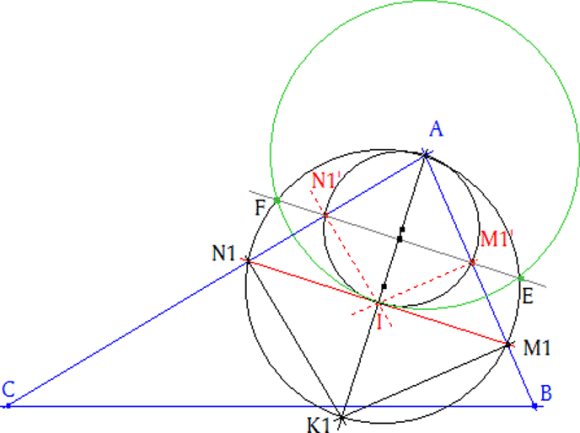
- Si observamos el cuadrilátero A, M1' ,I ,N1', como los ángulos en M1' y N1' son rectos entonces los ángulos en A y en I son suplementarios y por tanto el cuadrilátero es inscriptible en un círculo cuyo diámetro es AI.

- Si observamos el cuadrilátero A, M1 ,K1 ,N1, como los ángulos en M1 y N1 son rectos entonces los ángulos en A y en K1 son suplementarios y por tanto el cuadrilátero es inscriptible en un círculo cuyo diámetro es AK1.

Visto esto, podemos decir que estos dos últimos círculos también son homotéticos por la homotecia anterior.

- Efectuamos una inversión con respecto al círculo (verde) de centro en A y que pase por I,

- El círculo de diámetro AI se convierte en la perpendicular por I a AI y el de diámetro AK1 en la recta EF.

- M1' debe estar sobre AB y sobre EF; a su vez, EF es homotética de M1N1 entonces M1' es a la vez la imagen de M1 por la homotecia y anti-imagen de M1 por la inversión. Análogamente para N1' y N1.

- M1', I, N1' están sobre un mismo círculo; su inversa es una recta y por lo tanto M1, I y N1 están sobre una misma recta. A su vez I está sobre la bisectriz y M1 y N1 equidistan de A, entonces I es el punto medio de M1N1.

- Igualmente, permutando los vértices, vemos que el punto medio de M2N2 y de M3N3 también es I.

Por tanto podemos concluir que:

M1N1, M2N2, M3N3 TIENEN EL PUNTO MEDIO COMÚN Y ESE PUNTO ES EL INCENTRO DEL TRIÁNGULO ABC