Problema 160

En un triángulo isósceles el ortocentro está en la circunferencia inscrita.
Determina los ángulos.

Propuesto por el profesor Ricard Peiró del IES número 1 de Cheste.

V. Gúsiev y otros (1989). “Prácticas para resolver Problemas matemáticos. Geometría”. Ed. Mir. Página 45.

Solución de F. Damián Aranda Ballesteros,  profesor del IES Blas Infante de Córdoba.

Sea el triángulo isósceles ABC, de lados iguales AC = AB = b y base BC = a, con el ángulo <BAC= 2a. 

Del enunciado del problema deducimos la semejanza de los triángulos rectángulos siguientes:

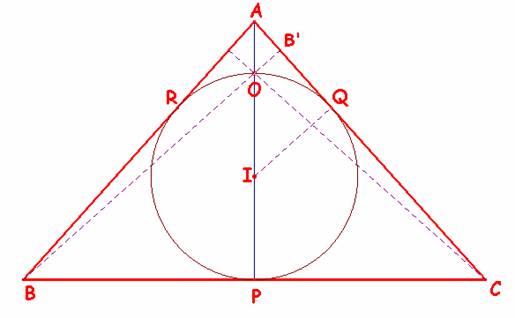El triángulo BB’C es semejante al APC, siendo iguales a a los ángulos en B y A.
Por tanto el triángulo BOP, semejante al BB’C, lo será también al triángulo AIQ con ángulos <IAQ = <PBO = a

 

 Así de la semejanza entre BOP y AIQ obtenemos que .
Por tanto BP=2.AQ, o lo que es lo mismo, ,
donde 2p = (perímetro) =2b+a.

Así tenemos que
Luego entonces:          

Considerando ahora el triángulo rectángulo APC, tenemos que:
.
Por tanto, el ángulo en la base del triángulo isósceles ABC es: <C = <B = arc cos 2/3