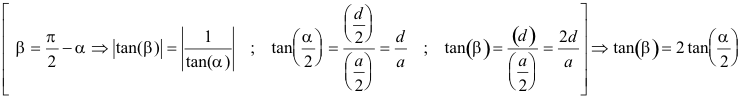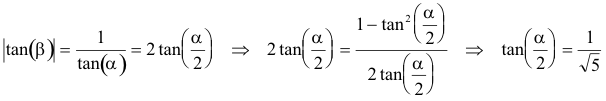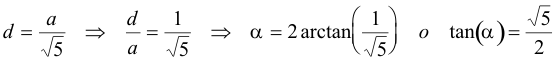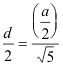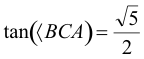Propuesto por el profesor Ricard Peiró del IES número 1 de Cheste

Problema 160 - En un triángulo isósceles el ortocentro está en la circunferencia inscrita.

Determina los ángulos.

V. Gúsiev y otros (1989). "Prácticas para resolver Problemas matemáticos. Geometría" Ed. Mir. Pàgina 45.

Solución de José María Pedret. Ingeniero naval. (Esplugas de Llobregat, Barcelona), 3 de abril de 2004

Las condiciones del enunciado exigen que la altura del ortocentro H sea igual al diámetro del círculo inscrito

¿Por qué?

Porque al ser el triángulo isósceles, el ortocentro está sobre la altura desde A a la base a.

Y por la misma razón, el centro I del círculo inscrito está sobre la misma altura.

Por lo tanto H está en la intersección del círculo inscrito y la altura desde A.

Una intersección es el punto medio de la base (trivial) y la otra la diametralmente opuesta.

Podemos pues trazar la figura imaginando el problema resuelto:

- la base del triángulo = a,

- el diámetro del círculo circunscrito = d

- AC el lado del triángulo isósceles

- BH una perpendicular por B a AC

Estudiando la figura, observamos las siguientes relaciones:

pero

 que nos da

Podemos trazar la

SOLUCION

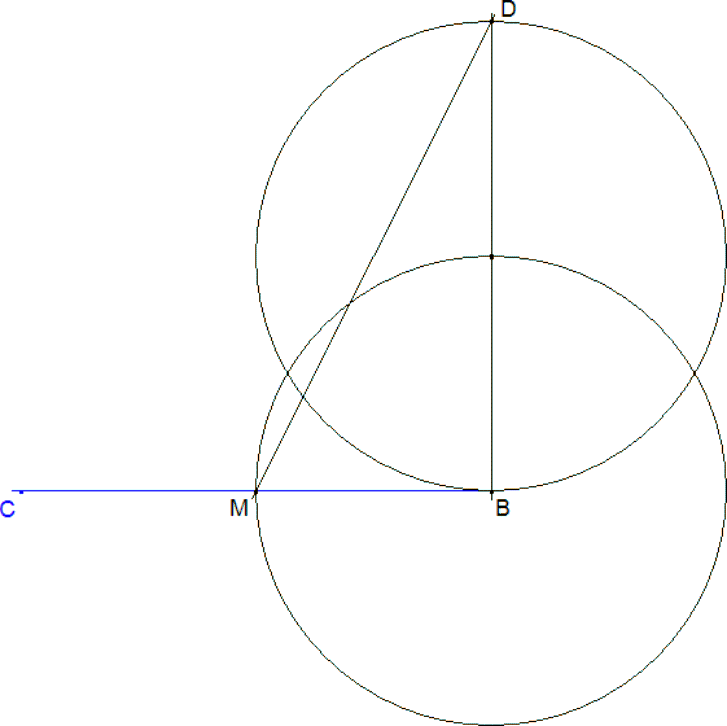
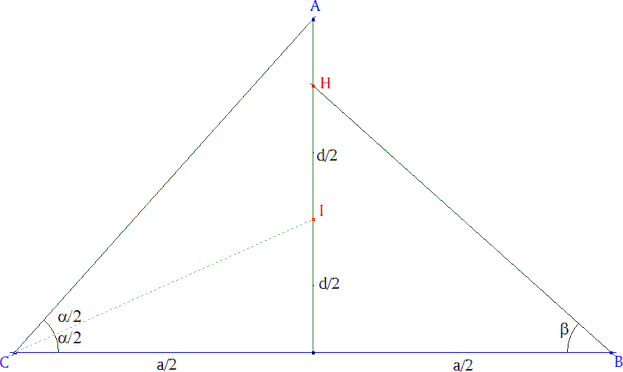
DETERMINCION DE LA RELACION

- Por un punto C trazamos CB = a

- Trazamos DB perpendicular a CB con DB=CB

- Unimos M, el punto medio de CB, con D

MBD es rectángulo DB/MB = 2 y MD² = MB²+DB² = MB²+(2 MB)² = 5MB²

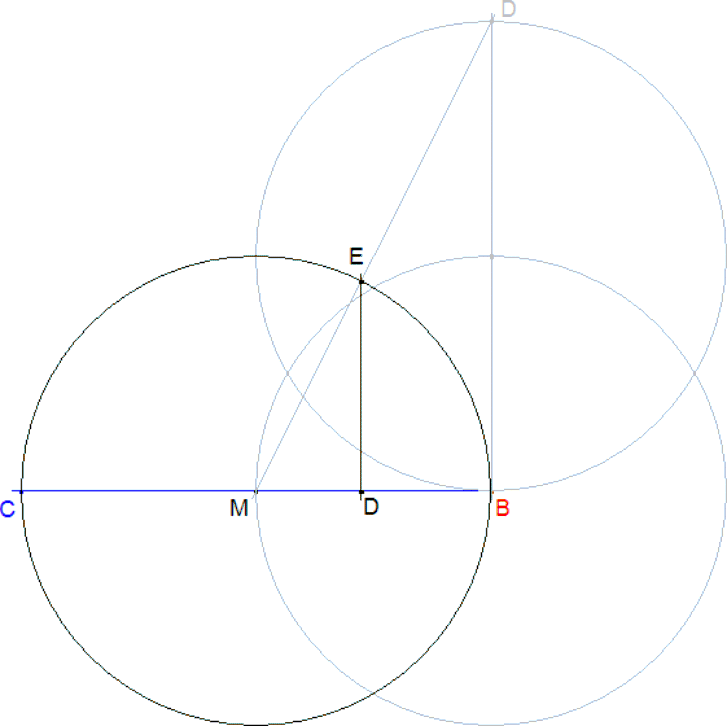
DETERMINCION DE

Si en lugar de tomar a tomamos a/2 obtendremos el radio del círculo circunscrito en lugar del diámetro.

- Con centro M trazamos el círculo de radio MB = a/2 que corta a MD en E. ME = a/2

- Paralela a DB por E que corta a MB en D. MD = d/2.

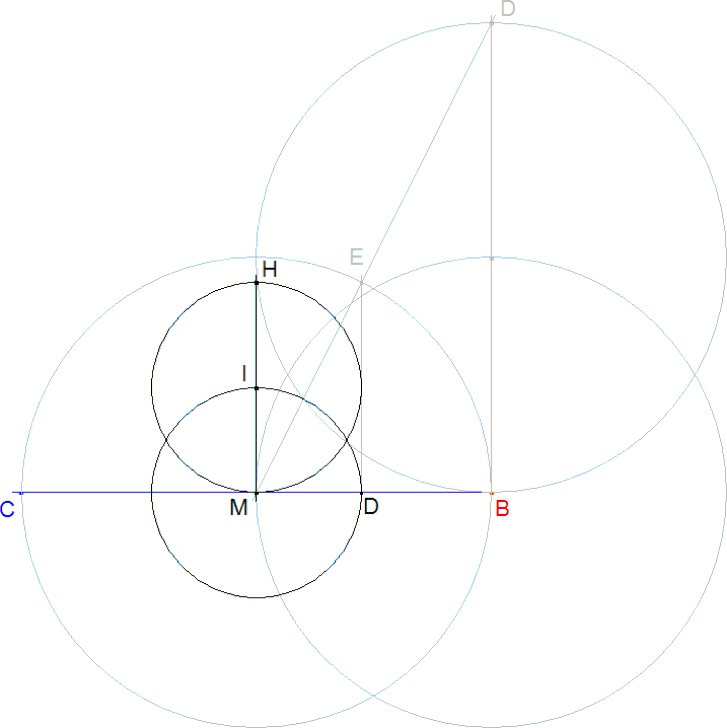
EL CIRCULO CIRCUNSCRITO Y EL ORTOCENTRO

Como hemos determinado MD = d/2

- Círculo con centro en M y radio MD

- Perpendicular por M a CB, corta al último círculo en I. I es el incentro.

- Con centro en I y radio IM trazamos el círculo inscrito, que vuelve a cortar a IM en H. H es el ortocentro.

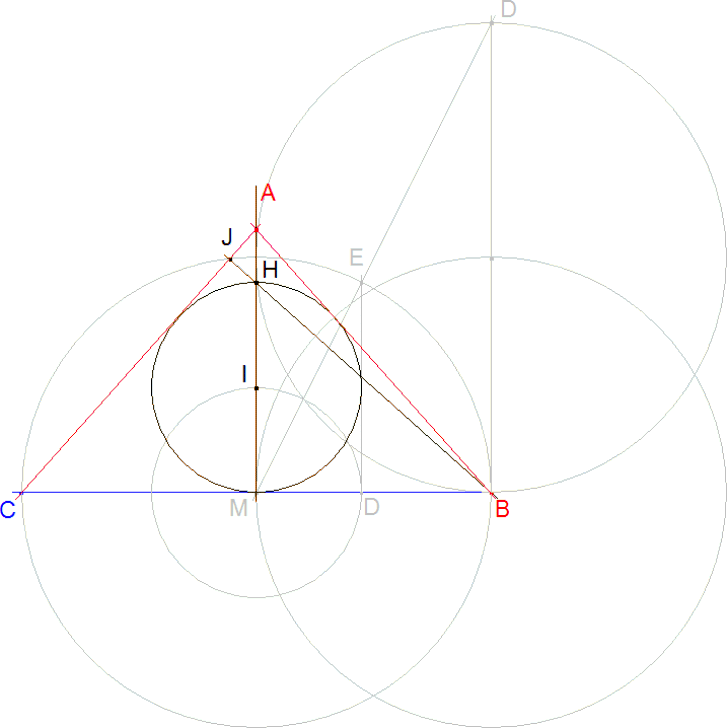
EL TRIANGULO

Como tenemos el círculo circunscrito podríamos trazar la segunda tangente desde C al círculo; pero para aprovechar parte del trabajo hecho, ya tenemos el ortocentro H. La recta BH es perpendicular a AC y corta a AC en la intersección J con el círculo de diámetro BC .

- BH corta al círculo de diámetro BC en J.

- La recta C J corta a HI en A.

 Dibujamos el triángulo ABC y el ángulo cumple