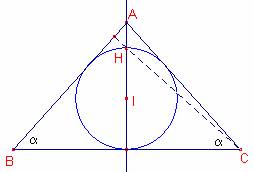
En un triángulo isósceles el ortocentro está en la circunferencia inscrita.
Determinar los ángulos.
V. Gúsiev y otros "Prácticas para resolver Problemas matemáticos. Geometría" Ed. Mir.1989. Página 45.
Solución deRicard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)(1 de abril de 2004) (en español)
Solución:
Consideremos el triángulo isósceles 
,
situados
en el plano cartesiano.
Sea 
el incentro.
El ortocentro tiene que estar en la perpendicular del lado desigual.
Por tanto 
.
Consideremos el vector 
Consideremos el vector 
Los vectores 
son perpendiculares,
entonces su producto escalar es cero.
, por tanto,
(1)
Sea la recta f que pasa por los puntos A, C que tiene por ecuación:
. Simplificándola:
La distancia del incentro I a la recta f es igual al radio r de la circunferencia inscrita, por tanto:
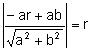, elevando
al cuadrado, 
(2)
Consideremos el sistema formado por (1) i (2)
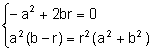
Resolviéndolo en las incógnitas a, b queda:
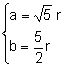
Siga 
,
.
, entonces,
